Planckov zakon sevanja

Izračun gostote moči sončnega sevalnega spektra

Erik Margan

Oddelek za eksperimentalno fiziko osnovnih delcev

Institut Jožef Stefan, Ljubljana

Max Planck je v svojem članku objavljenem leta 1901 (glej vire) podal podrobno izpeljavo spektralne zakonitosti sevanja idealnega črnega telesa v odvisnosti od absolutne temperature. Na osnovi tega je mogoče izračunati sevanje Sonca, ali katerega koli drugega telesa, katerega površina seva kot črno telo, pa tudi vsakega drugega telesa z upoštevanjem ustreznega korekcijskega faktorja v odvisnosti od barve sevalne površine.

Obratno, na osnovi meritev spektra, ali le valovne dolžine pri kateri ima sevanje maksimum je mogoče določiti tudi temperaturo telesa ki seva. Na podlagi geometrije sevalnega polja pa je mogoče določiti tudi celotno moč in energijo sevanja.

Zakon najpogosteje podajamo v obliki specifične sevalne moči [W] na enoto sevalne površine [m²], na enoto prostorskega kota (1 steradian), in na spektralno ločljivost (pri meritvah v okolici vidnega dela spektra ponavadi privzamemo da je ločljivost podana z valovno dolžino dλ = 1nm, oziroma 10^–9m, in sicer v območju med 10^–7m in 10^–5m). Simbolično to zgleda takole:

ρ_P(λ,T) dλ = 2hc²λ^–5 (e^hc/kTλ – 1)^–1 dλ ................................................. (1)

pri čemur je:

 ρ_P → spektralna gostota sevalne moči [W m^–2 sr^–1 nm^–1];

 λ → valovna dolžina sevanja [nm];

 T → absolutna temperatura telesa ki seva [K];

 h = 6,6260687652×10^–34 [Js] — Planckova energijska konstanta;

 c = 299792458 [m/s] — svetlobna hitrost;

 k = 1,380650324×10^–23 [J/K] — Boltzmanova termodinamična konstanta;

 e = 2,18281828459045 — Eulerjeva konstanta, oziroma naravno število.

Številk ni nujno pdajati tako precizno, zadostovale bi le 3 ali 4 decimalke, vendar bo računanje opravil računalnik, ki vedno računa s 16 decimalnih mest, vnos teh konstant v rutino pa je enkratno opravilo.

Če pa želimo dobiti energijsko sevalno gostoto, je treba gostoto moči množiti s faktorjem 4π, ter deliti s c:

ρ_W(λ,T) dλ = (4π/c) ρ_P(λ,T) dλ ........................................................... (2)

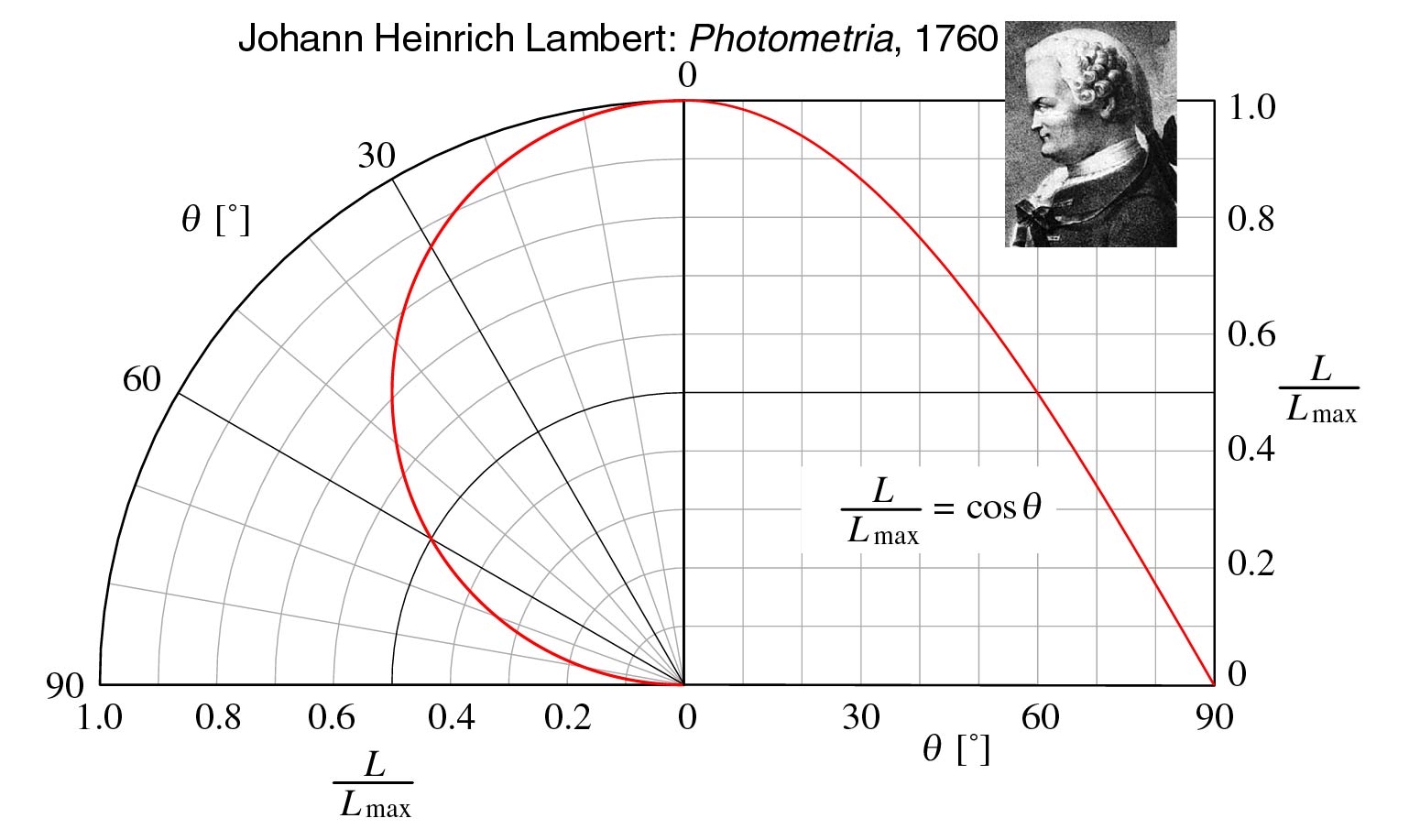
Pozor! Med tako normirano gostoto moči (oziroma energije) in Stefan-Boltzmannovim zakonom j = σT⁴ obstaja razlika v definicijah, ker je j definiran za sevanje površinske enote, ki seva v polkrogelni prostor, ali 2π steradiana (površina krogle je 4π sr). Zato se pogosto zgodi napaka, da zgornji enačbi množimo s 2π, toda treba je upoštevati še Lambertovo kotno odvisnost sevanja, ker enota površine seva v okolico sorazmerno cosθ (torej največ v smeri navpično na površino in nič v smeri vsporedno s površino), oziroma ∫cosθdθ v mejah med –π/2 in +π/2, kar je enako 2, torej je treba zgornji enačbi množiti le s π.

Sl.1: Prikaz Lambertove kotne odvisnosti sevanja v polarnih in pravokotnih koordinatah. Seveda je θ prostorski kot, čeprav je v diagramu narisan ravninski med 0 in 90°.

Izračun gostote moči za Sonce, ki seva pri povprečni temperaturi površja T = 5777K prikazuje Sl.2:

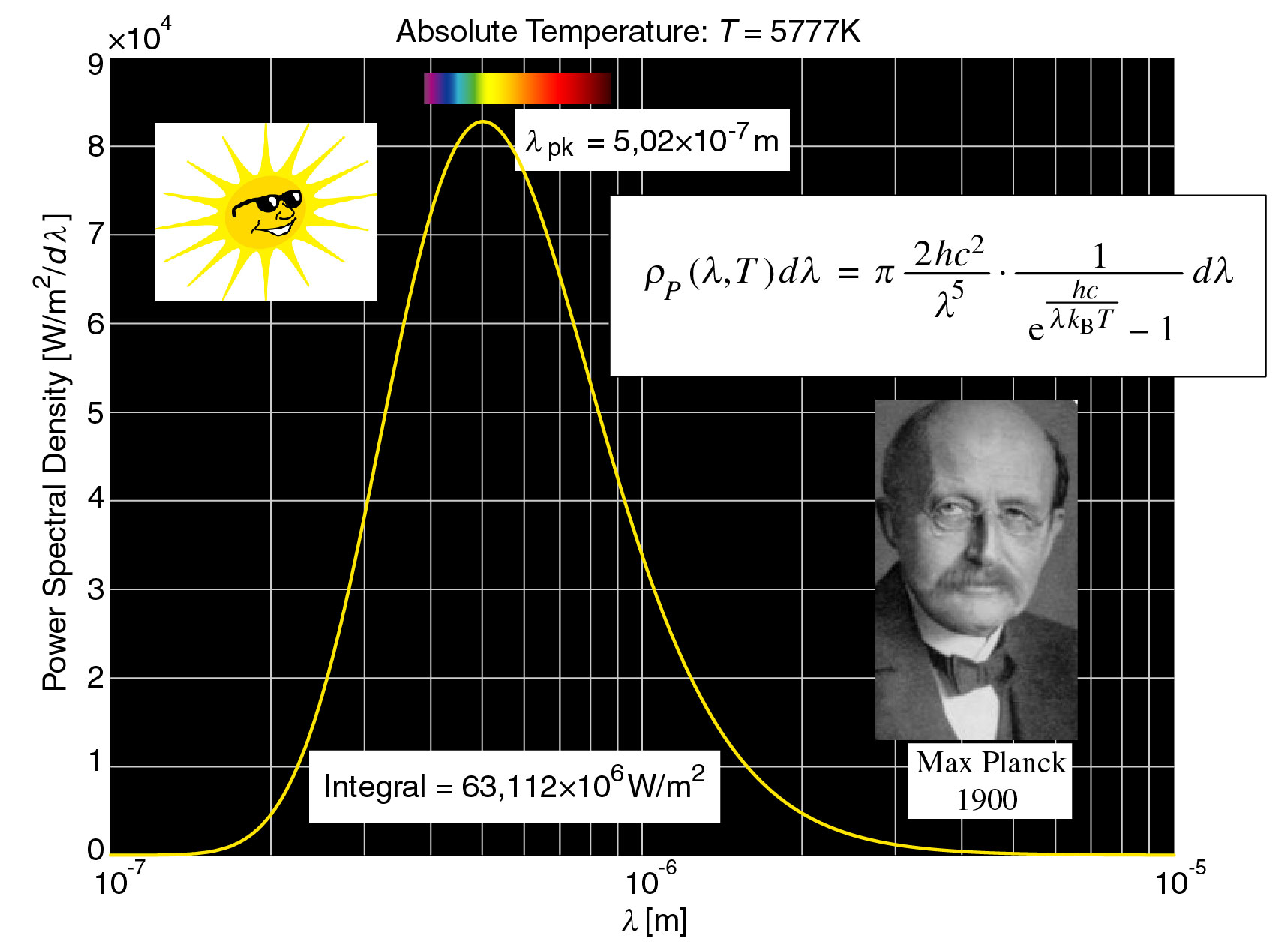
Sl.2: Spektralna porazdelitev gostote sevalne moči v odvisnosti od valovne dolžine (λ) ob temperaturi T = 5777K. Relacija za gostoto sevalne moči je normirana za primer 1m² sevalne površine ki v pasu dλ = 1nm seva kot Lambertov vir v prostorski kot 2π steradiana.

Če dobljeno porazdelitev integriramo po valovni dolžini dobimo, da vsak m² površine Sonca seva z močjo okoli 63MW. Seveda intenziteta sevanja pada s kvadratom oddaljenosti. Da bi izračunali koliko sevalne moči dobi vsak m² površine Zemlje, je treba celotno specifično sevalno moč množiti s celotno sevalno površino Sonca in nato deliti s površino krogle, katere radij je oddaljenost Zemlje od Sonca. Ker je površina krogle A = 4πr², se pri deljenju obeh površin faktor 4π pokrajša in ostane le ulomek kvardatov obeh radiev. Premer Sonca znaša d = 1,3927×10⁹m, oddaljenost Zemlje od Sonca pa je R = 1.496×10¹¹m, torej je gostota sevanja na Zemlji manjša za (d/2R)² = 2.1667×10^–5. Ko s to številko množimo integral 63,112×10⁶, dobimo sevalno gostoto moči na Zemlji, ali kot strokovno pravimo „solarno konstanto“, ki znaša 1366W/m².

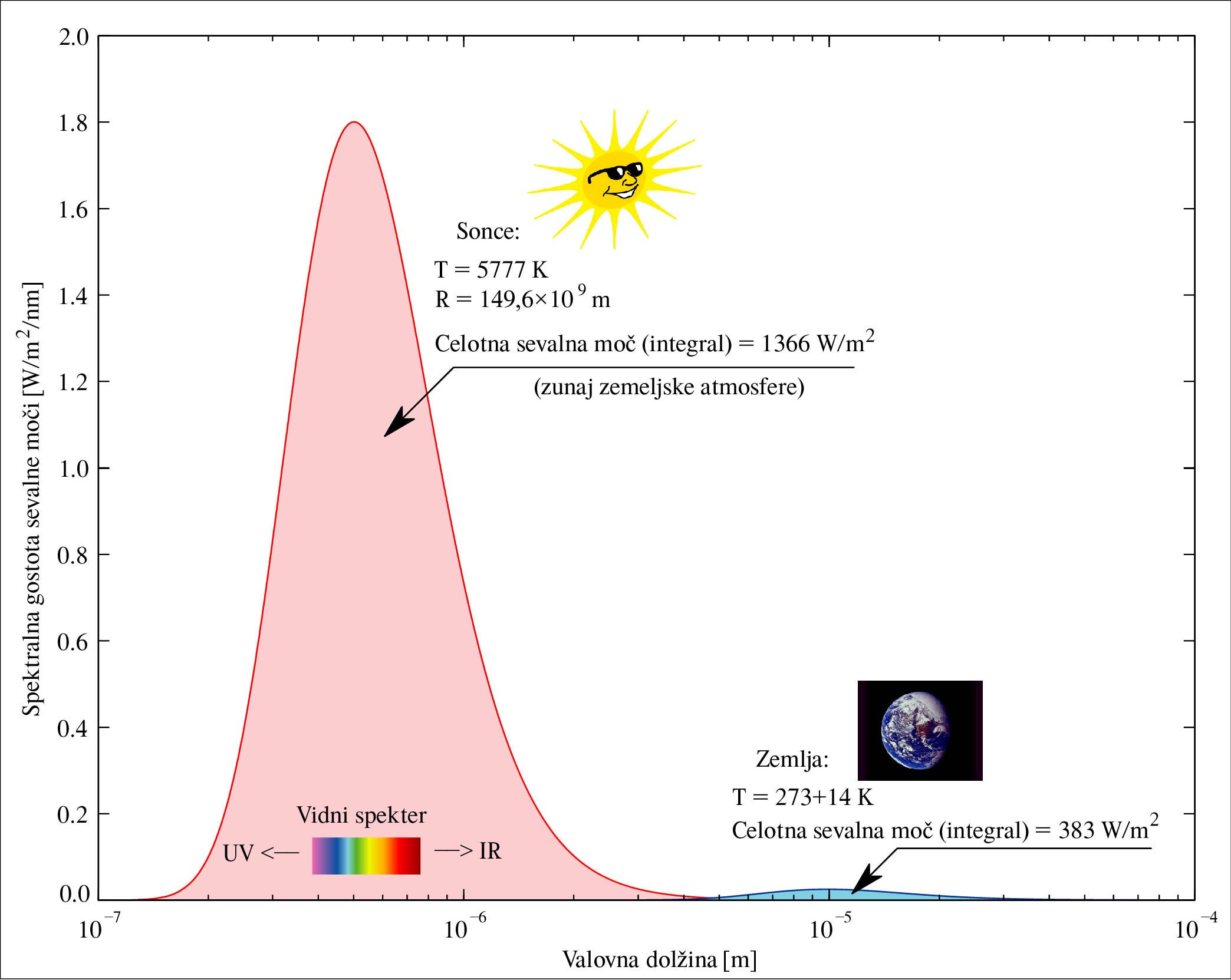
Sl.3: Primerjava sevalnih spektrov Sonca na razdalji zemeljske orbite in Zemlje ob povprečni temperaturi 14°C. Celotna sevalna moč na kvadratni meter površine je enaka integralu spektralne funkcije (poviršina pod krivuljo).

Zemeljska orbita pa ni krog temveč elipsa, zato se R med letom spreminja od ~152 milijonov kilometrov na dan 3. julija do ~147 milijonov kilometrov na dan 3. januarja. Temu primerno se spreminja tudi efektivno sevanje Sonca. Številka ki smo jo uporabili za R pa je letno povprečje. Zaradi nagnjenosti zemeljske rotacijske osi glede na orbitalno ravnino za ~23° dobi južna polobla v povprečju več energije kot severna, toda ta učinek je delno kompenziran z porazdelitvijo kopenskih in oceanskih površin, južna polobla ima precej večjo površino oceana, ki ima večjo tolotno kapaciteto, zato so temperaturni ekstremi nekoliko manjši..

Na Sl.4 pa je podrobneje prikazano termično sevanje zemeljskega površja pri različnih temperaturah (od –60°C do +50°C).

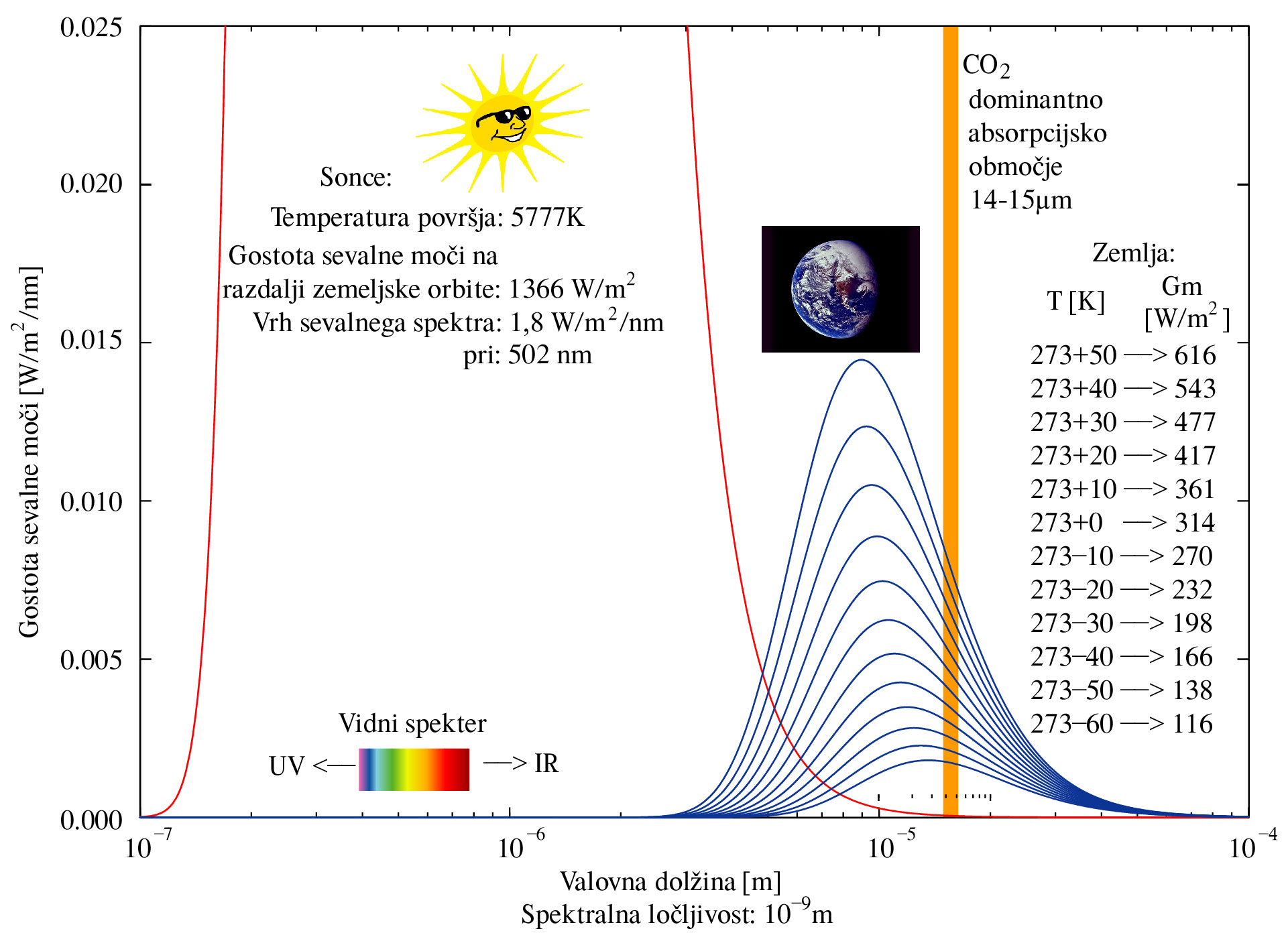
Sl.4: Podrobnejši prikaz slike 3 za sevalni spekter zemeljskega površja pri različnih temperaturah. Oranžna površina označuje dominantno absorpcisjko območje CO₂ (~14–15 µm valovne dolžine).

Najprej je treba opaziti, da se sevalni spekter površja ob povišani temperaturi odmika od absorpcijskega spektra CO₂, ki je praktično neodvisen od temperature ozračja: če je pri nizkih temperaturah absorpcijski spekter blizu vrha sevalnega spektra, je pri visokih temperaturah pri le ~1/2 od vrha. Zaradi tega CO₂ ne absorbira sevanje sorazmerno s toploto površja! To pomeni da ni mogoče najprej izračunati neko letno ali dolgoletno povprečno temperaturo in potem na podlagi tega skušati med seboj termalno uravnovesiti sončno sevanje in zemeljsko sevanje. Tople površine pač sevajo sorazmerno manj v dominantnem absorpcijskem območju CO₂ med 14–15 µm valovne dolžine.

Druga pomembna opomba je da gre pri absorpciji za verjetnost da neka molekula zajame foton. To pomeni da je pri določeni gostoti fotonov zelo pomemba tudi gostota posameznega plina v ozračju. Če bi bila zemeljska atmosfera sestavljena izključno iz CO₂, bi pri nizkih temperaturah površja bila atmosferska absorpcija okoli 6–7% celotnega sevalnega spektra, pri višjih pa le okoli 3–4%. Ker pa je delež CO₂ v atmosferi le ~0.04% gre velik delež fotonov v velike višine predno jih zajame kakšna molekula CO₂. Posledično absorpcija CO₂ prispeva segrevanju nižjih plasti zraka le malenkostno! Poleg tega ni dovolj da molekula CO₂ zajame foton, mora tudi trčiti v sosendo molekulo zraka in ji oddati del sprejete energije, šele s tem se toplota prenese na pline, ki sicer nimajo karakterističnih resonanc v tem delu spektra. Ko pa se to zgodi, ostane molekuli CO2 manj energije, ki se je spontano znebi po trku, zato bo emitirani foton tudi imel manjšo energijo, oziroma daljšo valovno dolžino, in ga nobena molekula CO₂ ne bo več zajela. Če pa molekula CO₂ odda foton pred trkom s kakšno drugo molekulo, bo ta foton imel sicer enako energijo kot absorbirani, vendar je verjetnost da bo emitiran proti površju le ½, pa še obstaja verjetnost da ga prestreže kaka druga molekula CO₂ predno doseže površje, in potem spet obstaja verjetnost le ½ da bo ta foton emitiran proti površju. Itd. Skratka, že navadna statistika govori proti domnevi o „pozitivni povratni zanki“, kot jo propagira IPCC.

Še vedno pa obstaja problem izračuna termalnega ravnovesja. Za pravilen izračun bi bilo treba najprej izračunati površinske deleže na različnih temperaturah in na podlagi teh določiti deleže sevalne moči različnih površin. Šele potem bi lahko izračunali povprečno sevalno moč (po metodi korena iz vsote kvadratov!) in iz povprečne sevalne moči s četrtim korenom dobiti efektivno povprečno temperaturo. Tega pa seveda nihče ne naredi, bodisi ker ni zanesljivih in celovitih podatkov (zaradi že omenjene težave s satelitskimi meritvami, ter redki pokritosti terena s merilnimi postajami), bodisi ker je račun nezanesljiv zaradi različnih in spreminjajočih se površn Zemlje (zaraščenost, puščave, padavine, albedo, ...), ali pa ker je izračun za marsikoga prezapleten!

Nekateri to upravičujejo tudi tako da rečejo da je mogoče časovne spremembe temperature razčleniti v Fourijerjevo vrsto, pri čemur se potem osnovna perioda ujema z vrtenjem Zemlje, ki se dolgočasovno izpovpreči v nič, druga harmonska komponenta pa dominantno prispeva k ogrevanju, med tem ko naj bi višje harmonske komponente lahko zanemarili (ker so spremembe temperature razmeroma počasne), zaradi česar napaka v izračunih zaradi neustreznega povprečenja ne bi smela biti večja od 2%. Prvi očitek takemu razmišljanju je ta, da se različne površine segrevajo in ohlajajo različno hitro, zato v primeru večjih in hitrejših nihanj prispevajo višje harmoske mkomponente sorazmerno več. Drugi očitek pa je ta, da je celotni trend v segrevanju ozračja v zadnjih 50 letih mogoče pripisati spremembi v energijski bilanci velikostnega reda +0,04% na leto, to pa je mnogo manj od tistih 2%, in tudi manj od sprememb v sončevi sevalni „konstanti“ (+/–0,07% v vidnem delu spektra, nekaj več v UV), ki je posledica 11-letnega aktivnostnega ciklusa.

Na koncu tega prispevka je podana rutina za izračun Planckovega sevalnega spektra prirejena za računalniški program Matlab <http://www.mathworks.com/products/matlab/>, ki jo lahko uporabimo tudi za izračun sevanja katerega koli toplega telesa, treba je le vstaviti zahtevano temperaturo in ustrezno območje valovnih dolžin. Denimo za izračun sevanja človeškega telesa lahko privzamemo absolutno temperaturo 273+36,7 = 309,7K in vstavimo srednjo valovno dolžino 10^–5m, okoli katere bo algoritem sam postavil meje valovnih dolžin za dekado višje in nižje, 10^–6m in 10^–4m, ter narisal graf spektralne porazdelitve sevalne moči. Ukaz v programu Matlab s katerim poženemo izračun se glasi preprosto takole:

M=PlanckRad(1e-5, 273+36.7);

Pozor: V slovenščini je v navadi da kot decimalno ločilo uporabljamo vejico, Matlab pa je ameriški program in tam je v navadi decimalna pika, med tem ko je vejica ločilo med argumenti funkcije! Prav tako decimalne eksponente pišemo kot v prikazanem primeru, torej število 10^–5 zapišemo kot 1e-5. Podrobnosti o operatorjih in programski sintaksi dobite, če poženete Matlab in vtipkate »help .«. Navodila o opcijah, ki so na voljo pri klicanju rutine dobite, če vtipkate »help PlanckRad«.

Viri:

Planck, Max:

Über das Gesetz der Energieverteilung im Normalspektrum

Annalen der Physik vol. 4: pp553 ff (1901)

Angleški prevod na spletu:

On the Law of Distribution of Energy in the Normal Spectrum

<http://theochem.kuchem.kyoto-u.ac.jp/Ando/planck1901.pdf>

Več informacij na Wikipediji:

<http://en.wikipedia.org/wiki/Planck%27s_law>

Računalniška rutina za izračun sevalnega spektra prirejena za program Matlab:

(če jo želite uporabljati, jo prekopirajte in shranite v \Matlab\work mapo

z imenom »PlanckRad.m«)

function M=PlanckRad(Lambda,Temp,plt,vers)

% PlanckRad Draws the power density spectrum of the radiation

%           emitted by a 1m^2 surface of an ideal black body

%           at temperature Temp [K], radiating as a Lambertian

%           source into a half sphere (2pi steradians).

%

%           Cal:  M=PlanckRad(Lambda, Temp, plt, vers);

%

%           where:

%           Lambda = [Lambda_min, Lambda_max, delta_Lambda]

%                    is the wavelength range and resolution;

%                    in case of a single input value use:

%                    Lambda = [Lambda/10, 10*Lambda];

%                    and delta_Lambda = 1nm;

%             Temp = absolute temperature [K]

%              plt = optional plotting parameter:

%                    3 for log(M) vs log(lambda) plot

%                    2 for log(M) vs lin(lambda) plot

%                    1 for lin(M) vs log(lambda) plot

%                    0 for lin(M) vs lin(lambda) plot;

%             vers = optional selection, power or energy density;

%                    3 for energy density with log-spaced Lambda

%                    2 for power density with log-spaced Lambda

%                    1 for energy density with delta_Lambda = 1nm

%                    0 for power density with delta_Lambda = 1nm;

%                M = energy or power spectral density.

% Author: Erik Margan, IJS, 20040527

% no copyright protection applied, free to use.

if nargin < 4

    % default: calculate power density spectrum

    vers=0;

end

if nargin < 3

    % default: plot linear vertical, log horizontal scale

    plt = 1 ;

end

if length(Lambda) < 2

    % default: 2 decade span, central Lambda given

    Lambda=[Lambda/10, 10*Lambda];

end

if length(Lambda) < 3

    % default: delta_Lambda=1nm

    delta_Lambda=1e-9;

    Lambda=[Lambda, delta_Lambda];

end

if vers > 1

    % use log-spaced Lambda, 1000 points

    lam=logspace(log10(Lambda(1)),log10(Lambda(2)), 1000);

else

    % use linear-spaced Lambda

    lam=(Lambda(1):Lambda(3):Lambda(2));

end

% constants:

h=6.6260687652e-34; % [Js] - Planck's constant

c=299792458; % [m/s] - speed of light

kB=1.380650324e-23; % [J/K] - Boltzman constant

% default: calculate power density

C1=2*h*(c^2);

if (vers == 1) | (vers == 3)

    % calculate energy density

    C1=C1*4*pi/c;

end

C2=h*c/(kB*Temp);

M=C1*(lam.^(-5))./(exp(C2 ./lam)-1);

% multiply by appropriate delta_Lambda

if vers > 1

    M=M.*[(lam(2)-lam(1)),diff(lam)];

else

    M=M.*delta_Lambda;

end

% correct for radiation into 2pi steradian, but observe

% the Lambert's cosine law, so multiply only by pi:

M=pi*M;

% find peak wavelength

x=find(M==max(M));

% find integral of M

Mtot=sum(M);

if plt == 3

    loglog(lam,M)

elseif plt == 2

    semilogy(lam,M)

elseif plt == 1

    semilogx(lam,M)

else

    plot(lam,M)

end

xlabel('wavelength [m]');

if (vers == 0) | (vers == 2)

    ylabel('Power Spectral Density [W/m^2/delta_Lambda]');

else

    ylabel('Energy Spectral Density [J/m^2/_delta_Lambda]');

end

title(['Absolute Temperature: T = ', num2str(Temp), ' K']);

text(1.02*lam(x), 0.95*max(M), ['lambda pk = ', num2str(lam(x)), ' m']);

if (vers == 2) | (vers == 0)

    text(lam(x), max(M)*0.25, ['Integral = ', num2str(Mtot), ' W/m^2']);

else

    text(lam(x), max(M)*0.25, ['Integral = ', num2str(Mtot), ' J/m^2']);

end