Ljubljana, avgust 1997
Naloga 1
Pokazi, da je kineticna energija p in n v jedru sorazmerna 
, ce jih obravnavas kot Fermijev plin (zapolnjeni so vsi nivoji do Fermijeve
energije 
)! Pri tem je n stevilo nukleonov, R pa radij volumna, v katerem se nahajajo.
Upostevaj, da je stevilo stanj podano z
Ob predpostavki, da je kineticna energija sorazmerna gornjemu izrazu
izpelji mesalni clen v masni formuli, ki da pozitiven prispevek k masi
jeder z 
(primerjaj energijo jedra z Z protoni in N nevtroni z energijo
jedra, kjer je 
)!
Naloga 2
Zapisi konfiguracijo in izracunaj magnetne momente naslednjih jeder
v lupinskem modelu: 
, 
in 
!
Naloga 3
Izrazi razmerje presekov za 
in 
, ki potekajo preko mocne interakcije, kot funkcijo dveh razlicnih izospinskih
amplitud (ene, ki opisuje prehode preko izospina 1 in druge, ki opisuje
prehode preko izospina 0). Clebsch-Gordanovi koeficienti 
, ki jih potrebujes, da izrazis produkte enodelcnih valovnih funkcij s
stanji z dobro definirano velikostjo in tretjo komponento izospina, so:
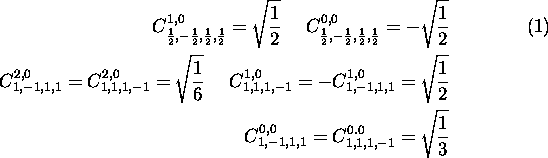
ima izospin 
in tretjo komponento 
, proton ima 
in 
, 
in 
pa imata I=1 in 
( 
in 
imata nasproten predznak 
).
Naloga 4
Ugotovi, kateri od naslednjih procesov so mozni, kateri potekajo preko sibke interakcije ter kateri so prepovedani. Pri dovoljenih narisi Feynmanove diagrame. Pri prepovedanih napisi, kateri ohranitveni zakon krsijo.
1: 
2: 
3: 
4: 
Kaksno razmerje pogostosti pricakujes za procesa 3 in 4?
5: 
; 
; 
; 
; 
, 
, 
, 
; 
.
Resitve nalog