Ljubljana, 26. junij 1997
Naloga 1
Pozitivno nabiti pioni ( 
) se elasticno sipajo na protonih preko resonance 
, ki ima spin J=3/2 ( 
). Kaksna je kotna porazdelitev sipanih pionov, ce si os z izberemo v smeri
vpadnih pionov? Predpostavi, da je tirna vrtilna kolicina vpadnih pionov 
=2, ter da je projekcija spina resonance
glede na os z M=1/2. Clebsch-Gordanovi koeficienti 
, ki dolocajo delez produkta enodelcnih valovnih funkcij z gibalnima kolicinama 
in 
ter projekcijama 
in 
v valovni funkciji s celotno gibalno kolicino J ter projekcijo M, znasajo: 
in 
. Potrebujes se krogelni funkciji 
, 
.
Naloga 2
Mezon 
je sestavljen iz para kvarkov 
, 
pa iz 
. Oba semileptonsko razpadata v elektron, elektronski nevtrino ter nabit
pion. Narisi Feynmanove diagrame za te razpade ter ugotovi, kateri delec
razpada v 
, kateri pa v 
!
Dolgoziva komponenta nevtralnega kaona 
je naslednja linearna kombinacija
in njegovega antidelca
:
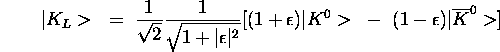
Z meritvijo razpadnih sirin za razpad
v
ter
lahko dolocimo parameter 
. Izrazi asimetrijo
kot funkcijo
! Pri tem upostevaj, da sta semileptonski razpadni sirini za razpad
in
enaki, ter da je 
. Koliksna je vrednost 
, ce je izmerjena asimetrija 
?
Naloga 3
Napovej maso vektorskega mezona 
(J=1, sestavljen iz para 
), ce poznas maso psevdoskalarnega mezona 
(J=0, sestavljen iz
), ki znasa 5279 MeV/c 
! Pri izracunu si pomagaj se s podatkom za masi vektorskega in psevdoskalarnega
mezona 
(J=1, M=2010 MeV/c
) in 
(J=0, M=1869 MeV/c
), sestavljenima iz para 
, ter podatkom o masi lahkih kvarkov u in d, ki znasa 310 MeV/c
.
Resitve nalog