class TGraph2D: public TNamed, public TAttLine, public TAttFill, public TAttMarker
Graph 2D class
This class has different constructors:
- With an array's dimension and three arrays x, y, and z:
TGraph2D *g = new TGraph2D(n, x, y, z);
x, y, z arrays can be doubles, floats, or ints. - With an array's dimension only:
TGraph2D *g = new TGraph2D(n);
The internal arrays are then filled with SetPoint. The following line fills the the internal arrays at the position "i" with the values x,y,z.g->SetPoint(i, x, y, z);
- Without parameters:
TGraph2D *g = new TGraph2D();
again SetPoint must be used to fill the internal arrays. - From a file:
TGraph2D *g = new TGraph2D("graph.dat");Arrays are read from the ASCII file "graph.dat" according to a specifies format. The format's default value is "%lg %lg %lg"
Specific drawing options can be used to paint a TGraph2D:
| "TRI" | The Delaunay triangles are drawn using filled area. An hidden surface drawing technique is used. The surface is painted with the current fill area color. The edges of each triangles are painted with the current line color. |
|---|---|
| "TRIW | The Delaunay triangles are drawn as wire frame |
| "TRI1 | The Delaunay triangles are painted with color levels. The edges of each triangles are painted with the current line color. |
| "TRI2 | the Delaunay triangles are painted with color levels. |
| "P" | Draw a marker at each vertex |
| "P0" | Draw a circle at each vertex. Each circle background is white. |
When a TGraph2D is drawn with one of the 2D histogram drawing option, a intermediate 2D histogram is filled using the Delaunay triangles technique to interpolate the data set.
TGraph2D linearly interpolate a Z value for any (X,Y) point given some existing (X,Y,Z) points. The existing (X,Y,Z) points can be randomly scattered. The algorithm works by joining the existing points to make Delaunay triangles in (X,Y). These are then used to define flat planes in (X,Y,Z) over which to interpolate. The interpolated surface thus takes the form of tessellating triangles at various angles. Output can take the form of a 2D histogram or a vector. The triangles found can be drawn in 3D.
This software cannot be guaranteed to work under all circumstances. They were originally written to work with a few hundred points in an XY space with similar X and Y ranges.
Example:
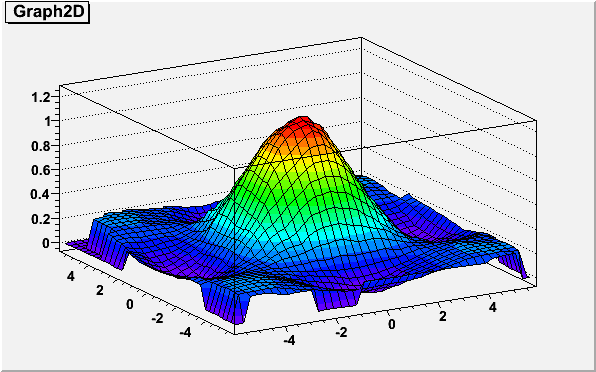
{
TCanvas *c = new TCanvas("c","Graph2D example",0,0,600,400);
Double_t x, y, z, P = 6.;
Int_t np = 200;
TGraph2D *dt = new TGraph2D();
TRandom *r = new TRandom();
for (Int_t N=0; N<np; N++) {
x = 2*P*(r->Rndm(N))-P;
y = 2*P*(r->Rndm(N))-P;
z = (sin(x)/x)*(sin(y)/y)+0.2;
dt->SetPoint(N,x,y,z);
}
gStyle->SetPalette(1);
dt->Draw("surf1");
return c;
}2D graphs can be fitted as shown by the following example:
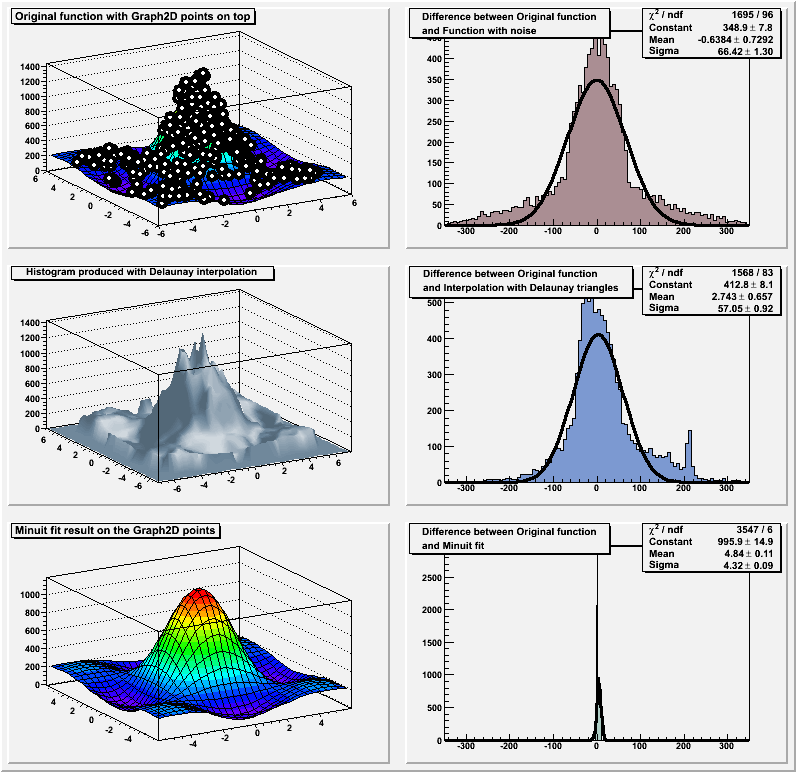
//Fitting a TGraph2D //Author: Olivier Couet #include <TMath.h> #include <TGraph2D.h> #include <TRandom.h> #include <TStyle.h> #include <TCanvas.h> #include <TF2.h> #include <TH1.h> TCanvas* graph2dfit() { gStyle->SetOptStat(0); gStyle->SetOptFit(); TCanvas *c = new TCanvas("c","Graph2D example",0,0,800,800); c->Divide(2,3); Double_t rnd, x, y, z; Double_t e = 0.3; Int_t nd = 400; Int_t np = 10000; TRandom r; Double_t fl = 6; TF2 *f2 = new TF2("f2","1000*(([0]*sin(x)/x)*([1]*sin(y)/y))+200",-fl,fl,-fl,fl); f2->SetParameters(1,1); TGraph2D *dt = new TGraph2D(); // Fill the 2D graph Double_t zmax = 0; for (Int_t N=0; N<nd; N++) { f2->GetRandom2(x,y); // Generate a random number in [-e,e] rnd = 2*r.Rndm()*e-e; z = f2->Eval(x,y)*(1+rnd); if (z>zmax) zmax = z; dt->SetPoint(N,x,y,z); } Double_t hr = 350; TH1D *h1 = new TH1D("h1", "#splitline{Difference between Original function}{and Function with noise}", 100, -hr, hr); TH1D *h2 = new TH1D("h2", "#splitline{Difference between Original function}{and Interpolation with Delaunay triangles}", 100, -hr, hr); TH1D *h3 = new TH1D("h3", "#splitline{Difference between Original function}{and Minuit fit}", 500, -hr, hr); f2->SetParameters(0.5,1.5); dt->Fit(f2); TF2 *fit2 = (TF2*)dt->FindObject("f2"); f2->SetParameters(1,1); for (Int_t N=0; N<np; N++) { f2->GetRandom2(x,y); // Generate a random number in [-e,e] rnd = 2*r.Rndm()*e-e; z = f2->Eval(x,y)*(1+rnd); h1->Fill(f2->Eval(x,y)-z); z = dt->Interpolate(x,y); h2->Fill(f2->Eval(x,y)-z); z = fit2->Eval(x,y); h3->Fill(f2->Eval(x,y)-z); } gStyle->SetPalette(1); c->cd(1); f2->SetTitle("Original function with Graph2D points on top"); f2->SetMaximum(zmax); gStyle->SetHistTopMargin(0); f2->Draw("surf1"); dt->Draw("same p0"); c->cd(3); dt->SetMargin(0.1); dt->SetFillColor(36); dt->SetTitle("Histogram produced with Delaunay interpolation"); dt->Draw("surf4"); c->cd(5); fit2->SetTitle("Minuit fit result on the Graph2D points"); fit2->Draw("surf1"); h1->SetFillColor(47); h2->SetFillColor(38); h3->SetFillColor(29); c->cd(2); h1->Fit("gaus","Q") ; h1->Draw(); c->cd(4); h2->Fit("gaus","Q") ; h2->Draw(); c->cd(6); h3->Fit("gaus","Q") ; h3->Draw(); c->cd(); return c; }
Definition of Delaunay triangulation (After B. Delaunay)
For a set S of points in the Euclidean plane, the unique triangulation DT(S) of S such that no point in S is inside the circumcircle of any triangle in DT(S). DT(S) is the dual of the Voronoi diagram of S. If n is the number of points in S, the Voronoi diagram of S is the partitioning of the plane containing S points into n convex polygons such that each polygon contains exactly one point and every point in a given polygon is closer to its central point than to any other. A Voronoi diagram is sometimes also known as a Dirichlet tessellation.
This applet gives a nice practical view of Delaunay triangulation and Voronoi diagram.
