class THistPainter: public TVirtualHistPainter

The histogram painter class

Introduction

Histograms are drawn via the THistPainter class. Each histogram has a pointer to its own painter (to be usable in a multithreaded program). When the canvas has to be redrawn, the Paint function of each objects in the pad is called. In case of histograms, TH1::Paint invokes directly THistPainter::Paint.

To draw a histogram "h" is enough to do: 

      h->Draw();
"h" can be of any kind: 1D, 2D or 3D. To choose how the histogram will be drawn, the Draw() method can be invoked with an option. For instance to draw a 2D histogram as a lego plot it is enough to do: 
      h->Draw("lego");
THistPainter offers many options to paint 1D, 2D and 3D histograms.

When the Draw() method of a histogram is called for the first time (TH1::Draw), it creates a THistPainter object and saves a pointer to this "painter" as a data member of the histogram. The THistPainter class specializes in the drawing of histograms. It is separated from the histogram so that one can have histograms without the graphics overhead, for example in a batch program. Each histogram have its own painter rather than a central singleton painter painting all histograms, allows two histograms to be drawn in two threads without overwriting the painter's values.

When a displayed histogram is filled again, there is not need to call the Draw() method again; the image will be refreshed the next time the pad will be updated.

A pad is updated after one of these three actions:

  1. a carriage control on the ROOT command line,
  2. a click inside the pad,
  3. a call to TPad::Update.

By default a call to TH1::Draw() clears the pad of all objects before drawing the new image of the histogram. One can use the "SAME" option to leave the previous display intact and superimpose the new histogram. The same histogram can be drawn with different graphics options in different pads.

When a displayed histogram is deleted, its image is automatically removed from the pad.

To create a copy of the histogram when drawing it, one can use TH1::DrawClone(). This will clone the histogram and allow to change and delete the original one without affecting the clone.

Histograms' plotting options

Most options can be concatenated with or without spaces or commas, for example: 
      h->Draw("E1 SAME");
The options are not case sensitive: 
      h->Draw("e1 same");
The default drawing option can be set with TH1::SetOption and retrieve using TH1::GetOption: 
      root [0] h->Draw();          // Draw "h" using the standard histogram representation.
      root [1] h->Draw("E");       // Draw "h" using error bars
      root [3] h->SetOption("E");  // Change the default drawing option for "h"
      root [4] h->Draw();          // Draw "h" using error bars
      root [5] h->GetOption();     // Retrieve the default drawing option for "h"
      (const Option_t* 0xa3ff948)"E"

Options supported for 1D and 2D histograms

"AXIS" Draw only axis.
"AXIG" Draw only grid (if the grid is requested).
"HIST" When an histogram has errors it is visualized by default with error bars. To visualize it without errors use the option HIST together with the required option (eg "hist same c"). The "HIST" option can also be used to plot only the histogram and not the associated function(s).
"FUNC" When an histogram has a fitted function, this option allows to draw the fit result only.
"SAME" Superimpose on previous picture in the same pad.
"CYL" Use Cylindrical coordinates. The X coordinate is mapped on the angle and the Y coordinate on the cylinder length.
"POL" Use Polar coordinates. The X coordinate is mapped on the angle and the Y coordinate on the radius.
"SPH" Use Spherical coordinates. The X coordinate is mapped on the latitude and the Y coordinate on the longitude.
"PSR" Use PseudoRapidity/Phi coordinates. The X coordinate is mapped on Phi.
"LEGO" Draw a lego plot with hidden line removal.
"LEGO1" Draw a lego plot with hidden surface removal.
"LEGO2" Draw a lego plot using colors to show the cell contents When the option "0" is used with any LEGO option, the empty bins are not drawn.
"SURF" Draw a surface plot with hidden line removal.
"SURF1" Draw a surface plot with hidden surface removal.
"SURF2" Draw a surface plot using colors to show the cell contents.
"SURF3" Same as SURF with in addition a contour view drawn on the top.
"SURF4" Draw a surface using Gouraud shading.
"SURF5" Same as SURF3 but only the colored contour is drawn. Used with option CYL, SPH or PSR it allows to draw colored contours on a sphere, a cylinder or a in pseudo rapidity space. In cartesian or polar coordinates, option SURF3 is used.
"TEXT" Draw bin contents as text (format set via gStyle->SetPaintTextFormat).
"TEXTnn" Draw bin contents as text at angle nn (0 < nn < 90).
"X+" The X-axis is drawn on the top side of the plot.
"Y+" The Y-axis is drawn on the right side of the plot.

Options supported for 1D histograms

" " Default.
"AH" Draw histogram without axis. "A" can be combined with any drawing option. For instance, "AC" draws the histogram as a smooth Curve without axis.
"][" When this option is selected the first and last vertical lines of the histogram are not drawn.
"B" Bar chart option.
"C" Draw a smooth Curve through the histogram bins.
"E" Draw error bars.
"E0" Draw error bars. Markers are drawn for bins with 0 contents.
"E1" Draw error bars with perpendicular lines at the edges.
"E2" Draw error bars with rectangles.
"E3" Draw a fill area through the end points of the vertical error bars.
"E4" Draw a smoothed filled area through the end points of the error bars.
"E5" Like E3 but ignore the bins with 0 contents.
"E6" Like E4 but ignore the bins with 0 contents.
"X0" When used with one of the "E" option, it suppress the error bar along X as gStyle->SetErrorX(0) would do.
"L" Draw a line through the bin contents.
"P" Draw current marker at each bin except empty bins.
"P0" Draw current marker at each bin including empty bins.
"PIE" Draw histogram as a Pie Chart.
"*H" Draw histogram with a * at each bin.
"LF2" Draw histogram like with option "L" but with a fill area. Note that "L" draws also a fill area if the hist fill color is set but the fill area corresponds to the histogram contour.
"9" Force histogram to be drawn in high resolution mode. By default, the histogram is drawn in low resolution in case the number of bins is greater than the number of pixels in the current pad.

Options supported for 2D histograms

" " Default (scatter plot).
"ARR" Arrow mode. Shows gradient between adjacent cells.
"BOX" A box is drawn for each cell with surface proportional to the content's absolute value. A negative content is marked with a X.
"BOX1" A button is drawn for each cell with surface proportional to content's absolute value. A sunken button is drawn for negative values a raised one for positive.
"COL" A box is drawn for each cell with a color scale varying with contents. All the none empty bins are painted. Empty bins are not painted unless some bins have a negative content because in that case the null bins might be not empty.
"COLZ" Same as "COL". In addition the color palette is also drawn.
"CONT" Draw a contour plot (same as CONT0).
"CONT0" Draw a contour plot using surface colors to distinguish contours.
"CONT1" Draw a contour plot using line styles to distinguish contours.
"CONT2" Draw a contour plot using the same line style for all contours.
"CONT3" Draw a contour plot using fill area colors.
"CONT4" Draw a contour plot using surface colors (SURF option at theta = 0).
"CONT5" (TGraph2D only) Draw a contour plot using Delaunay triangles.
"LIST" Generate a list of TGraph objects for each contour.
"FB" With LEGO or SURFACE, suppress the Front-Box.
"BB" With LEGO or SURFACE, suppress the Back-Box.
"A" With LEGO or SURFACE, suppress the axis.
"SCAT" Draw a scatter-plot (default).
"[cutg]" Draw only the sub-range selected by the TCutG named "cutg".

Options supported for 3D histograms

" " Default (scatter plot).
"ISO" Draw a Gouraud shaded 3d iso surface through a 3d histogram. It paints one surface at the value computed as follow: SumOfWeights/(NbinsX*NbinsY*NbinsZ).
"BOX" Draw a for each cell with volume proportional to the content's absolute value.
"LEGO" Same as BOX.

Options supported for histograms' stacks (THStack)

" " Default, the histograms are drawn on top of each other (as lego plots for 2D histograms).
"NOSTACK" Histograms in the stack are all paint in the same pad as if the option "SAME" had been specified.
"PADS" The current pad/canvas is subdivided into a number of pads equal to the number of histograms in the stack and each histogram is paint into a separate pad.

Setting the Style

Histograms use the current style (gStyle). When one changes the current style and would like to propagate the changes to the histogram, TH1::UseCurrentStyle should be called. Call UseCurrentStyle on each histogram is needed.
To force all the histogram to use the current style use: 
      gROOT->ForceStyle();
All the histograms read after this call will use the current style.

Setting line, fill, marker, and text attributes

The histogram classes inherit from the attribute classes: TAttLine, TAttFill, TAttMarker and TAttText. See the description of these classes for the list of options.

Setting Tick marks on the histogram axis

The TPad::SetTicks method specifies the type of tick marks on the axis. If tx = gPad->GetTickx() and ty = gPad->GetTicky() then: 
      tx = 1;   tick marks on top side are drawn (inside)
      tx = 2;   tick marks and labels on top side are drawn
      ty = 1;   tick marks on right side are drawn (inside)
      ty = 2;   tick marks and labels on right side are drawn
By default only the left Y axis and X bottom axis are drawn (tx = ty = 0)

TPad::SetTicks(tx,ty) allows to set these options. See also The TAxis functions to set specific axis attributes.

In case multiple color filled histograms are drawn on the same pad, the fill area may hide the axis tick marks. One can force a redraw of the axis over all the histograms by calling: 

      gPad->RedrawAxis();

Giving titles to the X, Y and Z axis

      h->GetXaxis()->SetTitle("X axis title");
      h->GetYaxis()->SetTitle("Y axis title");
The histogram title and the axis titles can be any TLatex string. The titles are part of the persistent histogram.

The option "SAME"

By default, when an histogram is drawn, the current pad is cleared before drawing. In order to keep the previous drawing and draw on top of it the option "SAME" should be use. The histogram drawn with the option "SAME" uses the coordinates system available in the current pad.

This option can be used alone or combined with any valid drawing option but some combinations must be use with care.

Limitations

  • It does not work when combined with the "LEGO" and "SURF" options unless the histogram plotted with the option "SAME" has exactly the same ranges on the X, Y and Z axis as the currently drawn histogram. To superimpose lego plots histograms' stacks should be used.

Superimposing two histograms with different scales in the same pad

The following example creates two histograms, the second histogram is the bins integral of the first one. It shows a procedure to draw the two histograms in the same pad and it draws the scale of the second histogram using a new vertical axis on the right side. See also the tutorial transpad.C for a variant of this example. 

Picture
Source



output of MACRO_THistPainter_1_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   // create/fill draw h1
   gStyle->SetOptStat(kFALSE);
   TH1F *h1 = new TH1F("h1","Superimposing two histograms with different scales",100,-3,3);
   Int_t i;
   for (i=0;i<10000;i++) h1->Fill(gRandom->Gaus(0,1));
   h1->Draw();
   c1->Update();

   // create hint1 filled with the bins integral of h1
   TH1F *hint1 = new TH1F("hint1","h1 bins integral",100,-3,3);
   Float_t sum = 0;
   for (i=1;i<=100;i++) {
      sum += h1->GetBinContent(i);
      hint1->SetBinContent(i,sum);
   }

   // scale hint1 to the pad coordinates
   Float_t rightmax = 1.1*hint1->GetMaximum();
   Float_t scale = gPad->GetUymax()/rightmax;
   hint1->SetLineColor(kRed);
   hint1->Scale(scale);
   hint1->Draw("same");

   // draw an axis on the right side
   TGaxis *axis = new TGaxis(gPad->GetUxmax(),gPad->GetUymin(),
   gPad->GetUxmax(), gPad->GetUymax(),0,rightmax,510,"+L");
   axis->SetLineColor(kRed);
   axis->SetTextColor(kRed);
   axis->Draw();
   return c1;
}
Statistics Display

The type of information shown in the histogram statistics box can be selected
with:

      gStyle->SetOptStat(mode);


The "mode" has up to nine digits that can be set to on(1 or 2), off(0).

      mode = iourmen  (default = 000001111)
      k = 1;  kurtosis printed
      k = 2;  kurtosis and kurtosis error printed
      s = 1;  skewness printed
      s = 2;  skewness and skewness error printed
      i = 1;  integral of bins printed
      o = 1;  number of overflows printed
      u = 1;  number of underflows printed
      r = 1;  rms printed
      r = 2;  rms and rms error printed
      m = 1;  mean value printed
      m = 2;  mean and mean error values printed
      e = 1;  number of entries printed
      n = 1;  name of histogram is printed


For example:

      gStyle->SetOptStat(11);


displays only the name of histogram and the number of entries, whereas:

      gStyle->SetOptStat(1101);


displays the name of histogram, mean value and RMS.

WARNING 1: never do:

      gStyle->SetOptStat(000111);


but instead do:

      gStyle->SetOptStat(1111);


because 0001111 will be taken as an octal number!

WARNING 2: for backward compatibility with older versions

      gStyle->SetOptStat(1);


is taken as:

      gStyle->SetOptStat(1111)


To print only the name of the histogram do:

      gStyle->SetOptStat(1000000001);


NOTE that in case of 2D histograms, when selecting only underflow
(10000) or overflow (100000), the statistics box will show all combinations
of underflow/overflows and not just one single number.

The parameter mode can be any combination of the letters
kKsSiourRmMen

      k :  kurtosis printed
      K :  kurtosis and kurtosis error printed
      s :  skewness printed
      S :  skewness and skewness error printed
      i :  integral of bins printed
      o :  number of overflows printed
      u :  number of underflows printed
      r :  rms printed
      R :  rms and rms error printed
      m :  mean value printed
      M :  mean value mean error values printed
      e :  number of entries printed
      n :  name of histogram is printed


For example, to print only name of histogram and number of entries do:

      gStyle->SetOptStat("ne");


To print only the name of the histogram do:

      gStyle->SetOptStat("n");


The default value is:

      gStyle->SetOptStat("nemr");



When a histogram is drawn, a TPaveStats object is created and added
to the list of functions of the histogram. If a TPaveStats object
already exists in the histogram list of functions, the existing object is just
updated with the current histogram parameters.

When a histogram is drawn with the option "SAME", the statistics box
is not drawn. To force the statistics box drawing with the option
"SAME", the option "SAMES" must be used.
If the new statistics box hides the previous statistics box, one can change
its position with these lines ("h" being the pointer to the histogram):

      Root > TPaveStats *st = (TPaveStats*)h->FindObject("stats")
      Root > st->SetX1NDC(newx1); //new x start position
      Root > st->SetX2NDC(newx2); //new x end position


To change the type of information for an histogram with an existing
TPaveStats one should do:

      st->SetOptStat(mode);


Where "mode" has the same meaning than when calling
gStyle->SetOptStat(mode) (see above).

One can delete the statistics box for a histogram TH1* h with:

      h->SetStats(0)


and activate it again with:

      h->SetStats(1).



Fit Statistics

The type of information about fit parameters printed in the histogram statistics
box can be selected via the parameter mode. The parameter mode can be
= pcev  (default = 0111)

      p = 1;  print Probability
      c = 1;  print Chisquare/Number of degrees of freedom
      e = 1;  print errors (if e=1, v must be 1)
      v = 1;  print name/values of parameters


Example:

      gStyle->SetOptFit(1011);


print fit probability, parameter names/values and errors.

    

  1.  When "v" = 1 is specified, only the non-fixed parameters are
     shown.

  2.  When "v" = 2 all parameters are shown.


Note: gStyle->SetOptFit(1) means "default value", so it is equivalent
to gStyle->SetOptFit(111)

The error bars options




"E"
Default. Shows only the error bars, not a marker.



"E1"
Small lines are drawn at the end of the error bars.



"E2"
Error rectangles are drawn.



"E3"
A filled area is drawn through the end points of the vertical error bars.



"E4"
A smoothed filled area is drawn through the end points of the vertical error
bars.



"E0"
Draw also bins with null contents.






Picture
Source



output of MACRO_THistPainter_3_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH1F *he = new TH1F("he","Distribution drawn with error bars (option E1)  ",100,-3,3);
   Int_t i;
   for (i=0;i<10000;i++) he->Fill(gRandom->Gaus(0,1));
   gStyle->SetEndErrorSize(3);
   gStyle->SetErrorX(1.);
   he->SetMarkerStyle(20);
   he->Draw("E1");
   return c1;
}
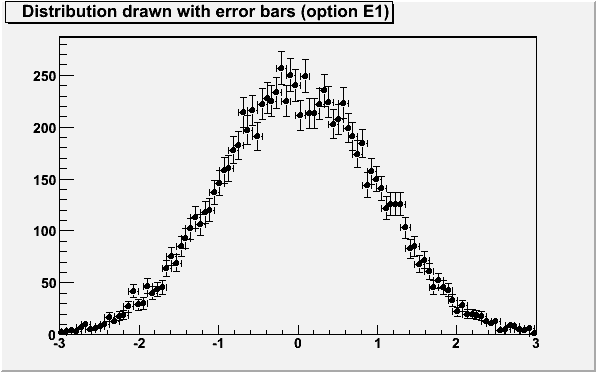
The options "E3" and "E4" draw an error band through the end points of the
vertical error bars. With "E4" the error band is smoothed. Because of the
smoothing algorithm used some artefacts may appear at the end of the band
like in the following example. In such cases "E3" should be used instead
of "E4".


Picture
Source



output of MACRO_THistPainter_5_ce4


{
   TCanvas *ce4 = new TCanvas("ce4","ce4",600,400);
   ce4->Divide(2,1);
   TH1F *he4 = new TH1F("he4","Distribution drawn with option E4",100,-3,3);
   Int_t i;
   for (i=0;i<10000;i++) he4->Fill(gRandom->Gaus(0,1));
   he4->SetFillColor(kRed);
   he4->GetXaxis()->SetRange(40,48);
   ce4->cd(1);
   he4->Draw("E4");
   ce4->cd(2);
   TH1F *he3 = he4->DrawClone("E3");
   he3->SetTitle("Distribution drawn option E3");
   return ce4;
}
The "BAR" and "HBAR" options

When the option "bar" or "hbar" is specified, a bar chart is drawn. A vertical
bar-chart is drawn with the options "bar", "bar0",
"bar1", "bar2", "bar3", "bar4".
An horizontal bar-chart is drawn with the options "hbar",
"hbar0", "hbar1", "hbar2", "hbar3",
"hbar4".

    

  •  The bar is filled with the histogram fill color.

  •  The left side of the bar is drawn with a light fill color.

  •  The right side of the bar is drawn with a dark fill color.

  •  The percentage of the bar drawn with either the light or dark color is:

      

    •     0% for option "(h)bar" or "(h)bar0"

    •    10% for option "(h)bar1"

    •    20% for option "(h)bar2"

    •    30% for option "(h)bar3"

    •    40% for option "(h)bar4"

    




Picture
Source



output of MACRO_THistPainter_7_c1


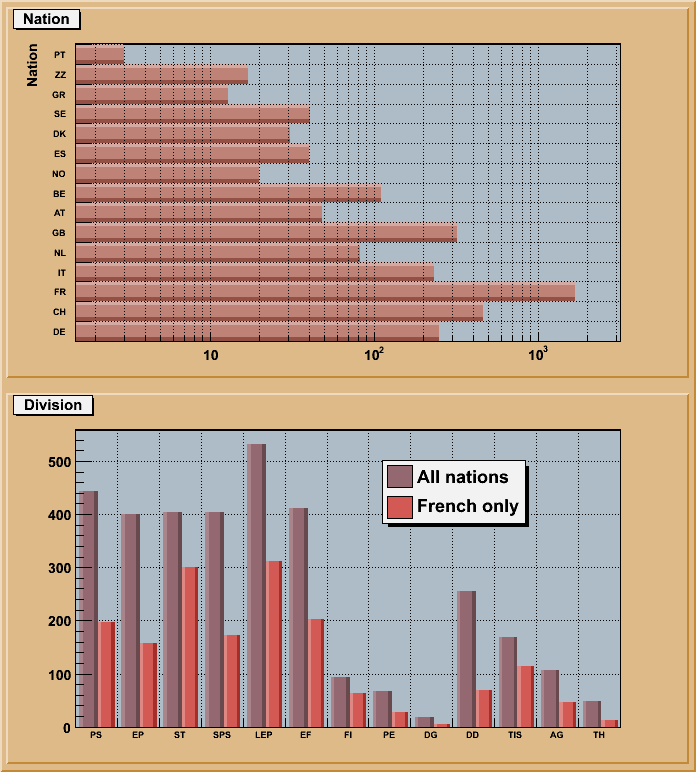
// Example of bar charts
// Author: Rene Brun
{
   TString dir = gSystem->UnixPathName(gInterpreter->GetCurrentMacroName());
   dir.ReplaceAll("hbars.C","../tree/cernbuild.C");
   dir.ReplaceAll("/./","/");
   if (!gInterpreter->IsLoaded(dir.Data())) gInterpreter->LoadMacro(dir.Data());
   TFile *f = (TFile*)gROOT->ProcessLineFast("cernbuild(1)");
   if (!f) return;
   TTree *T = (TTree*)f->Get("T");
   T->SetFillColor(45);
   TCanvas *c1 = new TCanvas("c1","histograms with bars",700,800);
   c1->SetFillColor(42);
   c1->Divide(1,2);
   
   //horizontal bar chart
   c1->cd(1); gPad->SetGrid(); gPad->SetLogx(); gPad->SetFrameFillColor(33);
   T->Draw("Nation","","hbar2");
   
   //vertical bar chart
   c1->cd(2); gPad->SetGrid(); gPad->SetFrameFillColor(33);
   T->Draw("Division>>hDiv","","goff");
   TH1F *hDiv   = (TH1F*)gDirectory->Get("hDiv");
   hDiv->SetStats(0);
   TH1F *hDivFR = (TH1F*)hDiv->Clone("hDivFR");
   T->Draw("Division>>hDivFR","Nation==\"FR\"","goff");
   hDiv->SetBarWidth(0.45);
   hDiv->SetBarOffset(0.1);
   hDiv->SetFillColor(49);
   TH1 *h1 = hDiv->DrawCopy("bar2");
   hDivFR->SetBarWidth(0.4);
   hDivFR->SetBarOffset(0.55);
   hDivFR->SetFillColor(50);
   TH1 *h2 = hDivFR->DrawCopy("bar2,same");
  
   TLegend *legend = new TLegend(0.55,0.65,0.76,0.82);
   legend->AddEntry(h1,"All nations","f");
   legend->AddEntry(h2,"French only","f");
   legend->Draw();
   
   c1->cd();
   delete f;
   return c1;
}
To control the bar width (default is the bin width) TH1::SetBarWidth()
should be used.


To control the bar offset (default is 0) TH1::SetBarOffset() should
be used.


These two parameters are useful when several histograms are plotted using
the option SAME. They allow to plot the histograms next to each other.

The SCATter plot option (default for 2D histograms)

For each cell (i,j) a number of points proportional to the cell content is
drawn. A maximum of kNMAX points per cell is drawn. If the maximum is above
kNMAX contents are normalized to kNMAX (kNMAX=2000).
If option is of the form "scat=ff", (eg scat=1.8,
scat=1e-3), then ff is used as a scale factor to compute the
number of dots. "scat=1" is the default.


Picture
Source



output of MACRO_THistPainter_9_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hscat = new TH2F("hscat","Option SCATter example (default for 2D histograms)  ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hscat->Fill(px,5*py);
      hscat->Fill(3+0.5*px,2*py-10.);
   }
   hscat->Draw("scat=0.5");
   return c1;
}
The ARRow option

Shows gradient between adjacent cells. For each cell (i,j) an arrow is drawn
The orientation of the arrow follows the cell gradient.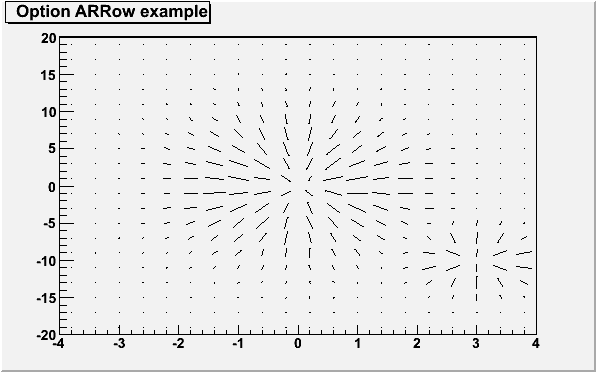


Picture
Source



output of MACRO_THistPainter_11_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *harr = new TH2F("harr","Option ARRow example",20,-4,4,20,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      harr->Fill(px,5*py);
      harr->Fill(3+0.5*px,2*py-10.,0.1);
   }
   harr->Draw("ARR");
   return c1;
}
The BOX option

For each cell (i,j) a box is drawn. The size (surface) of the box is
proportional to the absolute value of the cell content.
The cells with a negative content draw with a X on top of the boxes.


Picture
Source



output of MACRO_THistPainter_13_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   hbox  = new TH2F("hbox","Option BOX example",3,0,3,3,0,3);
   hbox->SetFillColor(42);
   hbox->Fill(0.5, 0.5,  1.);
   hbox->Fill(0.5, 1.5,  4.);
   hbox->Fill(0.5, 2.5,  3.);
   hbox->Fill(1.5, 0.5,  2.);
   hbox->Fill(1.5, 1.5, 12.);
   hbox->Fill(1.5, 2.5, -6.);
   hbox->Fill(2.5, 0.5, -4.);
   hbox->Fill(2.5, 1.5,  6.);
   hbox->Fill(2.5, 2.5,  0.5);
   hbox->Draw("BOX");
   return c1;
}
With option "BOX1" a button is drawn for each cell with surface
proportional to content's absolute value. A sunken button is drawn for
negative values a raised one for positive.


Picture
Source



output of MACRO_THistPainter_15_c1


{
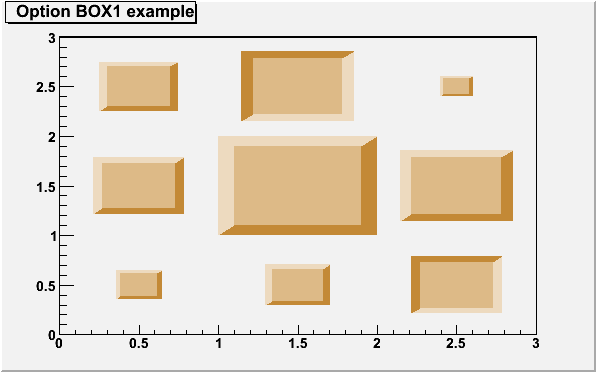
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   hbox1  = new TH2F("hbox1","Option BOX1 example",3,0,3,3,0,3);
   hbox1->SetFillColor(42);
   hbox1->Fill(0.5, 0.5,  1.);
   hbox1->Fill(0.5, 1.5,  4.);
   hbox1->Fill(0.5, 2.5,  3.);
   hbox1->Fill(1.5, 0.5,  2.);
   hbox1->Fill(1.5, 1.5, 12.);
   hbox1->Fill(1.5, 2.5, -6.);
   hbox1->Fill(2.5, 0.5, -4.);
   hbox1->Fill(2.5, 1.5,  6.);
   hbox1->Fill(2.5, 2.5,  0.5);
   hbox1->Draw("BOX1");
   return c1;
}
When the option "SAME" is used with the option "BOX", the
boxes' sizes are computing taking the previous plots into account. The range
along the Z axis is imposed by the first plot (the one without option
"SAME"); therefore the order in which the plots are done is relevant.


Picture
Source



output of MACRO_THistPainter_17_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hb1 = new TH2F("hb1","Example of BOX plots with option SAME ",40,-3,3,40,-3,3);
   TH2F *hb2 = new TH2F("hb2","hb2",40,-3,3,40,-3,3);
   TH2F *hb3 = new TH2F("hb3","hb3",40,-3,3,40,-3,3);
   TH2F *hb4 = new TH2F("hb4","hb4",40,-3,3,40,-3,3);
   for (Int_t i=0;i<1000;i++) {
      double x,y;
      gRandom->Rannor(x,y);
      if(x>0 && y>0) hb1->Fill(x,y,4);
      if(x<0 && y<0) hb2->Fill(x,y,3);
      if(x>0 && y<0) hb3->Fill(x,y,2);
      if(x<0 && y>0) hb4->Fill(x,y,1);
   }
   hb1->SetFillColor(1);
   hb2->SetFillColor(2);
   hb3->SetFillColor(3);
   hb4->SetFillColor(4);
   hb1->Draw("box");
   hb2->Draw("box same");
   hb3->Draw("box same");
   hb4->Draw("box same");
   return c1;
}
The COLor option

For each cell (i,j) a box is drawn with a color proportional to the cell
content.

The color table used is defined in the current style.

The color palette in TStyle can be modified via gStyle->SePalette().

All the none empty bins are painted. Empty bins are not painted unless
some bins have a negative content because in that case the null bins
might be not empty.

Combined with the option "COL", the option "Z" allows to
display the color palette defined by gStyle->SePalette().

In the following example, the histogram has only positive bins; the empty
bins (containing 0) are not drawn.


Picture
Source



output of MACRO_THistPainter_19_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcol1 = new TH2F("hcol1","Option COLor example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcol1->Fill(px,5*py);
   }
   gStyle->SetPalette(1);
   hcol1->Draw("COLZ");
   return c1;
}
In the following example, the histogram has some negative bins; the empty
bins (containing 0) are drawn.


Picture
Source



output of MACRO_THistPainter_21_c1


{
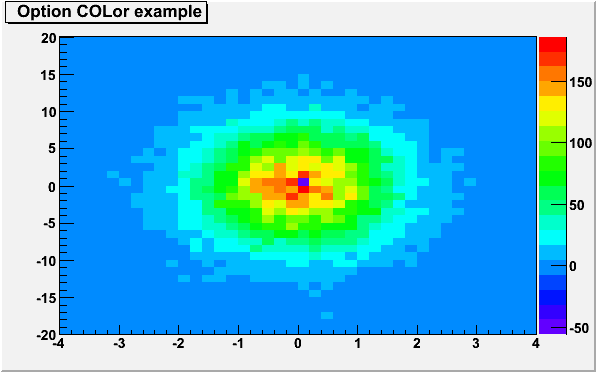
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcol2 = new TH2F("hcol2","Option COLor example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcol2->Fill(px,5*py);
   }
   hcol2->Fill(0,0,-200);
   gStyle->SetPalette(1);
   hcol2->Draw("COLZ");
   return c1;
}
The TEXT and TEXTnn Option

For each bin the content is printed. The text attributes are:

    

  •  text font = current TStyle font (gStyle->SetTextFont()).

  •  text size = 0.02*padheight*markersize.

  •  text color = marker color.


By default the format "g" is used. This format can be redefined
by calling gStyle->SetPaintTextFormat().

It is also possible to use "TEXTnn" in order to draw the text with
the angle nn (0 < nn < 90).

For 2D histograms the text is plotted in the center of each non empty cells.
For 1D histogram the text is plotted at a y position equal to the bin content.


Picture
Source



output of MACRO_THistPainter_23_c01


{
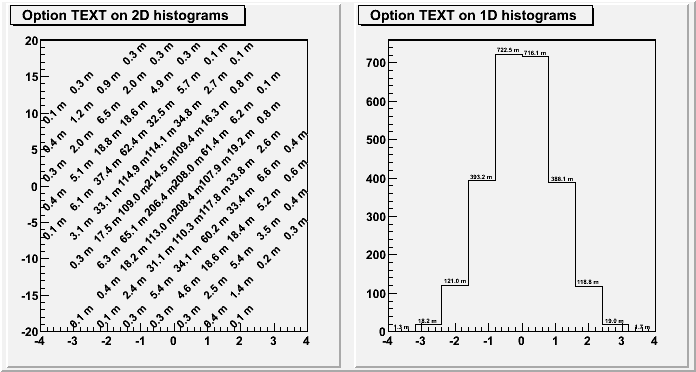
   TCanvas *c01 = new TCanvas("c01","c01",700,400);
   c01->Divide(2,1);
   TH1F *htext1 = new TH1F("htext1","Option TEXT on 1D histograms ",10,-4,4);
   TH2F *htext2 = new TH2F("htext2","Option TEXT on 2D histograms ",10,-4,4,10,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
        htext1->Fill(px,0.1);
      htext2->Fill(px,5*py,0.1);
   }
   gStyle->SetPaintTextFormat("4.1f m");
   htext2->SetMarkerSize(1.8);
   c01->cd(1);
   htext2->Draw("TEXT45");
   c01->cd(2);
   htext1->Draw();
   htext1->Draw("TEXT0 SAME");
   return c01;
}
The CONTour options

The following contour options are supported:



"CONT"
Draw a contour plot (same as CONT0).



"CONT0"
Draw a contour plot using surface colors to distinguish contours.



"CONT1"
Draw a contour plot using the line colors to distinguish contours.



"CONT2"
Draw a contour plot using the line styles to distinguish contours.



"CONT3"
Draw a contour plot solid lines for all contours.



"CONT4"
Draw a contour plot using surface colors ("SURF" option at theta = 0).



"CONT5"
Draw a contour plot using Delaunay triangles.




The following example shows a 2D histogram plotted with the option
"CONTZ". The option "CONT" draws a contour plot using surface
colors to distinguish contours.  Combined with the option "CONT" (or
"CONT0"), the option "Z" allows to display the color palette
defined by gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_25_c1


{
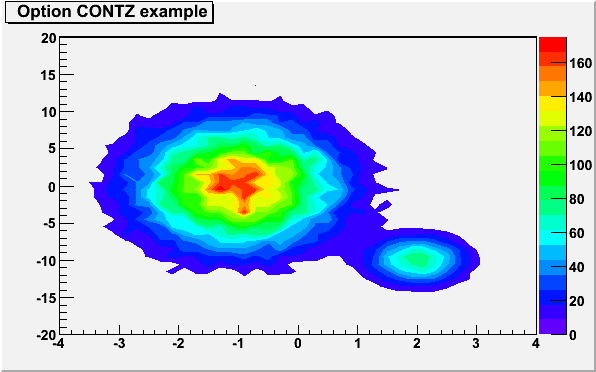
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcontz = new TH2F("hcontz","Option CONTZ example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcontz->Fill(px-1,5*py);
      hcontz->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   hcontz->Draw("CONTZ");
   return c1;
}
The following example shows a 2D histogram plotted with the option
"CONT1Z". The option "CONT1" draws a contour plot using the
line colors to distinguish contours. Combined with the option "CONT1",
the option "Z" allows to display the color palette defined by
gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_27_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcont1 = new TH2F("hcont1","Option CONT1Z example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcont1->Fill(px-1,5*py);
      hcont1->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   hcont1->Draw("CONT1Z");
   return c1;
}
The following example shows a 2D histogram plotted with the option
"CONT2". The option "CONT2" draws a contour plot using the
line styles to distinguish contours.


Picture
Source



output of MACRO_THistPainter_29_c1


{
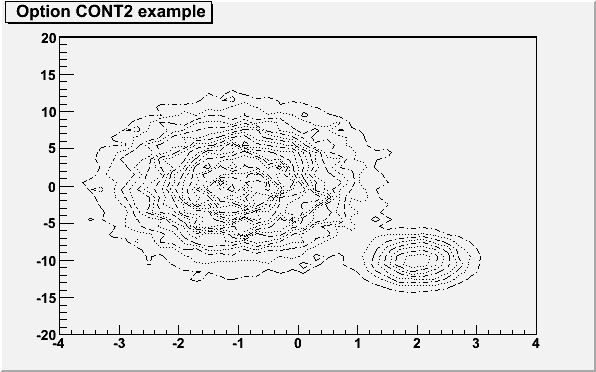
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcont2 = new TH2F("hcont2","Option CONT2 example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcont2->Fill(px-1,5*py);
      hcont2->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hcont2->Draw("CONT2");
   return c1;
}
The following example shows a 2D histogram plotted with the option
"CONT3". The option "CONT3" draws contour plot solid lines for
all contours.


Picture
Source



output of MACRO_THistPainter_31_c1


{
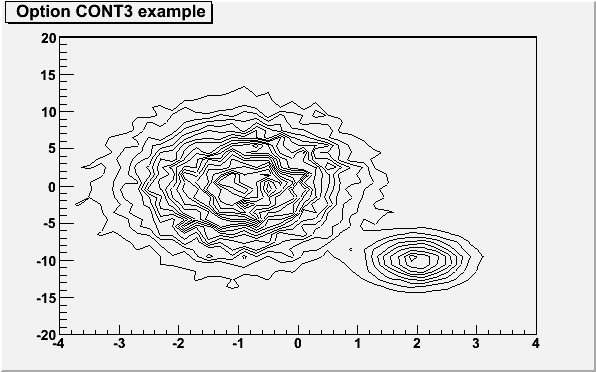
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcont3 = new TH2F("hcont3","Option CONT3 example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcont3->Fill(px-1,5*py);
      hcont3->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hcont3->Draw("CONT3");
   return c1;
}
The following example shows a 2D histogram plotted with the option
"CONT4". The option "CONT4" draws a contour plot using surface
colors to distinguish contours ("SURF" option at theta = 0). Combined
with the option "CONT" (or "CONT0"), the option "Z"
allows to display the color palette defined by gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_33_c1


{
   TCanvas *c1 = new TCanvas("c1","c1",600,400);
   TH2F *hcont4 = new TH2F("hcont4","Option CONT4Z example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hcont4->Fill(px-1,5*py);
      hcont4->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   hcont4->Draw("CONT4Z");
   return c1;
}
The default number of contour levels is 20 equidistant levels and can be changed
with TH1::SetContour() or TStyle::SetNumberContours().

When option "LIST" is specified together with option
"CONT", the points used to draw the contours are saved in
TGraph objects and are accessible in the following way:

      TObjArray *contours = gROOT->GetListOfSpecials()->FindObject("contours")
      Int_t ncontours     = contours->GetSize();
      TList *list         = (TList*)contours->At(i);


Where i is a contour number, and list contains a list of
TGraph objects.
For one given contour, more than one disjoint polyline may be generated.
The number of TGraphs per contour is given by:

      list->GetSize();


To access the first graph in the list one should do:

      TGraph *gr1 = (TGraph*)list->First();


The following example shows how to use this functionality.


Picture
Source



output of MACRO_THistPainter_35_c1


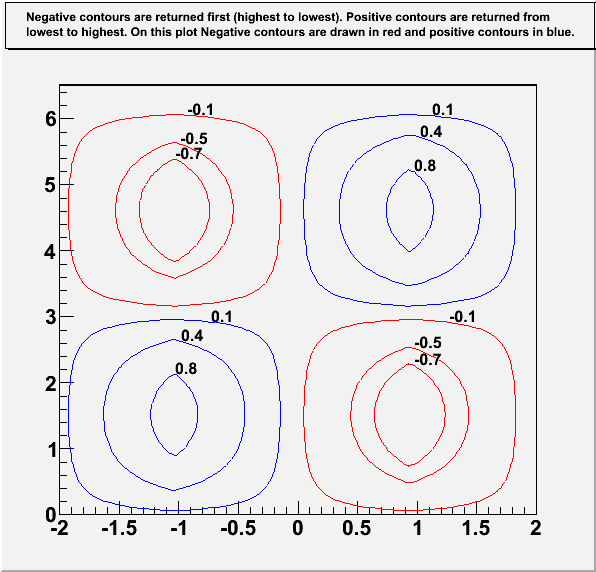
// TEST SCRIPT FOR: Getting Contours From TH2D
// Author: Josh de Bever
//         CSI Medical Physics Group
//         The University of Western Ontario
//         London, Ontario, Canada
//   Date: Oct. 22, 2004
//   Modified by O.Couet (Nov. 26, 2004)

TCanvas *ContourList(){
 
   const Double_t PI = TMath::Pi(); 
    
   TCanvas* c = new TCanvas("c","Contour List",0,0,600,600);
   c->SetRightMargin(0.15);
   c->SetTopMargin(0.15);
 
   Int_t i, j, TotalConts;
    
   Int_t nZsamples   = 80;
   Int_t nPhiSamples = 80;

   Double_t HofZwavelength = 4.0;       // 4 meters 
   Double_t dZ             =  HofZwavelength/(Double_t)(nZsamples - 1);
   Double_t dPhi           = 2*PI/(Double_t)(nPhiSamples - 1);
 
   TArrayD z(nZsamples);
   TArrayD HofZ(nZsamples);
   TArrayD phi(nPhiSamples);
   TArrayD FofPhi(nPhiSamples);

   
   // Discretized Z and Phi Values
   for ( i = 0; i < nZsamples; i++) {
      z[i] = (i)*dZ - HofZwavelength/2.0;
      HofZ[i] = SawTooth(z[i], HofZwavelength);
   }

   for(Int_t i=0; i < nPhiSamples; i++){
      phi[i] = (i)*dPhi;      
      FofPhi[i] = sin(phi[i]); 
   }

   // Create Histogram
   TH2D *HistStreamFn = new TH2D("HstreamFn", 
   "#splitline{Histogram with negative and positive contents. Six contours are defined.}{It is plotted with options CONT LIST to retrieve the contours points in TGraphs}", 
   nZsamples, z[0], z[nZsamples-1], nPhiSamples, phi[0], phi[nPhiSamples-1]);
     
   // Load Histogram Data
   for (Int_t i = 0; i < nZsamples; i++) {
      for(Int_t j = 0; j < nPhiSamples; j++){
         HistStreamFn->SetBinContent(i,j, HofZ[i]*FofPhi[j]);
      } 
   }

   gStyle->SetPalette(1); 
   gStyle->SetOptStat(0);
   gStyle->SetTitleW(0.99);
   gStyle->SetTitleH(0.08);
   
   Double_t contours[6];
   contours[0] = -0.7;
   contours[1] = -0.5;
   contours[2] = -0.1;
   contours[3] =  0.1;
   contours[4] =  0.4;
   contours[5] =  0.8;
     
   HistStreamFn->SetContour(6, contours); 
 
   // Draw contours as filled regions, and Save points
   HistStreamFn->Draw("CONT Z LIST");
   c->Update(); // Needed to force the plotting and retrieve the contours in TGraphs
    
   // Get Contours
   TObjArray *conts = (TObjArray*)gROOT->GetListOfSpecials()->FindObject("contours");
   TList* contLevel = NULL;
   TGraph* curv     = NULL;    
   Int_t nGraphs    = 0;
   Int_t TotalConts = 0;
    
   
   if (conts == NULL){
      printf("*** No Contours Were Extracted!\n");
      TotalConts = 0;
      return;
   } else {
      TotalConts = conts->GetSize();
   }

   printf("TotalConts = %d\n", TotalConts);
        
   for(i = 0; i < TotalConts; i++){       
      contLevel = (TList*)conts->At(i);
      printf("Contour %d has %d Graphs\n", i, contLevel->GetSize());
      nGraphs += contLevel->GetSize();
   }
    
   nGraphs = 0;
    
   TCanvas* c1 = new TCanvas("c1","Contour List",610,0,600,600);
   c1->SetTopMargin(0.15);
   TH2F *hr = new TH2F("hr",
   "#splitline{Negative contours are returned first (highest to lowest). Positive contours are returned from}{lowest to highest. On this plot Negative contours are drawn in red and positive contours in blue.}",
   2, -2, 2, 2, 0, 6.5);

   hr->Draw();
   Double_t x0, y0, z0;
   TLatex l;
   l.SetTextSize(0.03);
   char val[20];
   
   for(i = 0; i < TotalConts; i++){       
      contLevel = (TList*)conts->At(i);
      if (i<3) z0 = contours[2-i];
      else     z0 = contours[i];
      printf("Z-Level Passed in as:  Z = %f\n", z0);

      // Get first graph from list on curves on this level
      curv = (TGraph*)contLevel->First();
      for(j = 0; j < contLevel->GetSize(); j++){
         curv->GetPoint(0, x0, y0);
         if (z0<0) curv->SetLineColor(kRed);
         if (z0>0) curv->SetLineColor(kBlue);
         nGraphs ++;
         printf("\tGraph: %d  -- %d Elements\n", nGraphs,curv->GetN());
         curv->Draw("C");
         sprintf(val,"%g",z0);
         l.DrawLatex(x0,y0,val);
         curv = (TGraph*)contLevel->After(curv); // Get Next graph 
      }
   }
   c1->Update();
   printf("\n\n\tExtracted %d Contours and %d Graphs \n", TotalConts, nGraphs );
   gStyle->SetTitleW(0.);
   gStyle->SetTitleH(0.);
   return c1;
}


Double_t SawTooth(Double_t x, Double_t WaveLen){

// This function is specific to a sawtooth function with period
// WaveLen, symmetric about x = 0, and with amplitude = 1. Each segment
// is 1/4 of the wavelength.
//
//           |  
//      /\   |
//     /  \  |
//    /    \ |
//   /      \          
//  /--------\--------/------------
//           |\      /
//           | \    / 
//           |  \  /
//           |   \/
//

   Double_t y;
   if ( (x < -WaveLen/2) || (x > WaveLen/2)) y = -99999999; // Error X out of bounds
   if (x <= -WaveLen/4) {
      y = x + 2.0;
   } else if ((x > -WaveLen/4) && (x <= WaveLen/4)) {
      y = -x ;
   } else if (( x > WaveLen/4) && (x <= WaveLen/2)) {
      y = x - 2.0;
   }
   return y;
}
The following options select the "CONT4" option and are useful for
sky maps or exposure maps.



"AITOFF"
Draw a contour via an AITOFF projection.



"MERCATOR"
Draw a contour via an Mercator projection.



"SINUSOIDAL"
Draw a contour via an Sinusoidal projection.



"PARABOLIC"
Draw a contour via an Parabolic projection.






Picture
Source



output of MACRO_THistPainter_37_c1


{
  //this tutorial illustrate the special contour options
  //    "AITOFF"     : Draw a contour via an AITOFF projection
  //    "MERCATOR"   : Draw a contour via an Mercator projection
  //    "SINUSOIDAL" : Draw a contour via an Sinusoidal projection
  //    "PARABOLIC"  : Draw a contour via an Parabolic projection
  // 
  //Author: Olivier Couet (from an original macro sent by Ernst-Jan Buis)
    
   gStyle->SetPalette(1);
   gStyle->SetOptTitle(1);
   gStyle->SetOptStat(0);

   TCanvas *c1 = new TCanvas("c1","earth_projections",700,700);
   c1->Divide(2,2);

   TH2F *ha = new TH2F("ha","Aitoff",    180, -180, 180, 179, -89.5, 89.5);
   TH2F *hm = new TH2F("hm","Mercator",  180, -180, 180, 161, -80.5, 80.5);
   TH2F *hs = new TH2F("hs","Sinusoidal",180, -180, 180, 181, -90.5, 90.5);
   TH2F *hp = new TH2F("hp","Parabolic", 180, -180, 180, 181, -90.5, 90.5);

   TString dat = gSystem->UnixPathName(gInterpreter->GetCurrentMacroName());
   dat.ReplaceAll("C","dat");
   dat.ReplaceAll("/./","/");

   ifstream in;
   in.open(dat.Data());
   Float_t x,y;
   while (1) {
     in >> x >> y;
     if (!in.good()) break;
     ha->Fill(x,y, 1);
     hm->Fill(x,y, 1);
     hs->Fill(x,y, 1);
     hp->Fill(x,y, 1);
   }
   in.close();

   c1->cd(1); ha->Draw("aitoff");
   c1->cd(2); hm->Draw("mercator");
   c1->cd(3); hs->Draw("sinusoidal");
   c1->cd(4); hp->Draw("parabolic");

   return c1;
}
The LEGO options

In a lego plot the cell contents are drawn as 3-d boxes. The height of each box
is proportional to the cell content. The lego aspect is control with the
following options:



"LEGO" 
Draw a lego plot using the hidden lines removal technique.



"LEGO1"
Draw a lego plot using the hidden surface removal technique.



"LEGO2"
Draw a lego plot using colors to show the cell contents.



"0"
When used with any LEGO option, the empty bins are not drawn.




See the limitations with the option "SAME".


The following example shows a 2D histogram plotted with the option
"LEGO". The option "LEGO" draws a lego plot using the hidden
lines removal technique.


Picture
Source



output of MACRO_THistPainter_39_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hlego = new TH2F("hlego","Option LEGO example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hlego->Fill(px-1,5*py);
      hlego->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hlego->Draw("LEGO");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"LEGO1". The option "LEGO1" draws a lego plot using the
hidden surface removal technique. Combined with any "LEGOn" option, the
option "0" allows to not drawn the empty bins.


Picture
Source



output of MACRO_THistPainter_41_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hlego1 = new TH2F("hlego1","Option LEGO1 example (with option 0)  ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hlego1->Fill(px-1,5*py);
      hlego1->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   hlego1->SetFillColor(kYellow);
   hlego1->Draw("LEGO1 0");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"LEGO2". The option "LEGO2" draws a lego plot using colors to
show the cell contents.  Combined with the option "LEGO2", the option
"Z" allows to display the color palette defined by
gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_43_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hlego2 = new TH2F("hlego2","Option LEGO2Z example ",40,-4,4,40,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hlego2->Fill(px-1,5*py);
      hlego2->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   hlego2->Draw("LEGO2Z");
   return c2;
}
The "SURFace" options

In a surface plot, cell contents are represented as a mesh.
The height of the mesh is proportional to the cell content.



"SURF"
Draw a surface plot using the hidden line removal technique.



"SURF1"
Draw a surface plot using the hidden surface removal technique.



"SURF2"
Draw a surface plot using colors to show the cell contents.



"SURF3"
Same as SURF with in addition a contour view drawn on the top.



"SURF4"
Draw a surface using the Gouraud shading technique.




See the limitations with the option "SAME".


The following example shows a 2D histogram plotted with the option
"SURF". The option "SURF" draws a lego plot using the hidden
lines removal technique.


Picture
Source



output of MACRO_THistPainter_45_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hsurf = new TH2F("hsurf","Option SURF example ",30,-4,4,30,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hsurf->Fill(px-1,5*py);
      hsurf->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hsurf->Draw("SURF");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"SURF1". The option "SURF1" draws a surface plot using the
hidden surface removal technique.  Combined with the option "SURF1",
the option "Z" allows to display the color palette defined by
gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_47_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hsurf1 = new TH2F("hsurf1","Option SURF1 example ",30,-4,4,30,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hsurf1->Fill(px-1,5*py);
      hsurf1->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hsurf1->Draw("SURF1");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"SURF2". The option "SURF2" draws a surface plot using colors
to show the cell contents. Combined with the option "SURF2", the option
"Z" allows to display the color palette defined by
gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_49_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hsurf2 = new TH2F("hsurf2","Option SURF2 example ",30,-4,4,30,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hsurf2->Fill(px-1,5*py);
      hsurf2->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hsurf2->Draw("SURF2");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"SURF3". The option "SURF3" draws a surface plot using the
hidden line removal technique with, in addition, a contour view drawn on the
top.  Combined with the option "SURF3", the option "Z" allows
to display the color palette defined by gStyle->SePalette().


Picture
Source



output of MACRO_THistPainter_51_c2


{
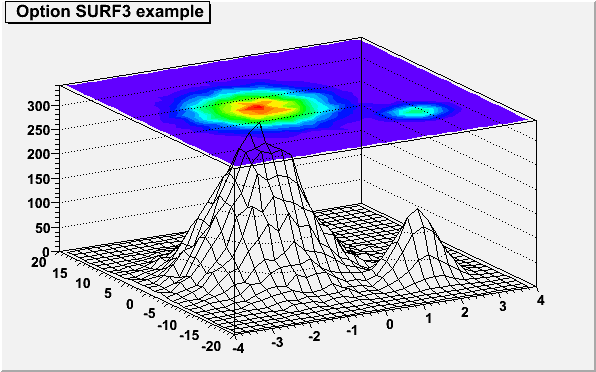
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hsurf3 = new TH2F("hsurf3","Option SURF3 example ",30,-4,4,30,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hsurf3->Fill(px-1,5*py);
      hsurf3->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hsurf3->Draw("SURF3");
   return c2;
}
The following example shows a 2D histogram plotted with the option
"SURF4". The option "SURF4" draws a surface using the Gouraud
shading technique.


Picture
Source



output of MACRO_THistPainter_53_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TH2F *hsurf4 = new TH2F("hsurf4","Option SURF4 example ",30,-4,4,30,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hsurf4->Fill(px-1,5*py);
      hsurf4->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hsurf4->SetFillColor(kOrange);
   hsurf4->Draw("SURF4");
   return c2;
}
As shown in the following example, when a contour plot is painted on top of a
surface plot using the option SAME, the contours appear in 3D on the
surface.


Picture
Source



output of MACRO_THistPainter_55_c2


{
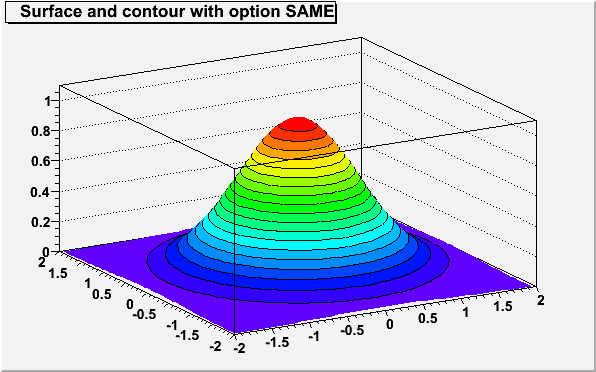
   TCanvas *c1=new TCanvas("c2","c2",600,400);
   int NBins = 50;
   double d = 2;
   TH2F* hsc = new TH2F("hsc", "Surface and contour with option SAME ", NBins, -d, d, NBins, -d, d);
   for (int bx = 1;  bx <= NBins; ++bx) {
      for (int by = 1;  by <= NBins; ++by) {
         double x = hsc->GetXaxis()->GetBinCenter(bx);
         double y = hsc->GetYaxis()->GetBinCenter(by);
         hsc->SetBinContent(bx, by, exp(-x*x)*exp(-y*y));
      }
   }
   gStyle->SetPalette(1);
   hsc->Draw("surf2");
   hsc->Draw("CONT1 SAME");
   return c2;
}
Cylindrical, Polar, Spherical and PseudoRapidity/Phi options

Legos and surfaces plots are represented by default in Cartesian coordinates.
Combined with any "LEGOn" or "SURFn" options the following
options allow to draw a lego or a surface in other coordinates systems.



"CYL"
Use Cylindrical coordinates. The X coordinate is mapped on the angle and the Y
coordinate on the cylinder length.



"POL"
Use Polar coordinates. The X coordinate is mapped on the angle and the Y
coordinate on the radius.



"SPH"
Use Spherical coordinates. The X coordinate is mapped on the latitude and the
Y coordinate on the longitude.



"PSR"
Use PseudoRapidity/Phi coordinates. The X coordinate is mapped on Phi.




WARNING: Axis are not drawn with these options.

The following example shows the same histogram as a lego plot is the four
different coordinates systems.


Picture
Source



output of MACRO_THistPainter_57_c3


{
   TCanvas *c3 = new TCanvas("c3","c3",600,400);
   c3->Divide(2,2);
   TH2F *hlcc = new TH2F("hlcc","Cylindrical coordinates",20,-4,4,20,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hlcc->Fill(px-1,5*py);
      hlcc->Fill(2+0.5*px,2*py-10.,0.1);
   }
   hlcc->SetFillColor(kYellow);
   c3->cd(1) ; hlcc->Draw("LEGO1 CYL");
   c3->cd(2) ; TH2F *hlpc = hlcc->DrawClone("LEGO1 POL");
   hlpc->SetTitle("Polar coordinates");
   c3->cd(3) ; TH2F *hlsc = hlcc->DrawClone("LEGO1 SPH");
   hlsc->SetTitle("Spherical coordinates");
   c3->cd(4) ; TH2F *hlprpc = hlcc->DrawClone("LEGO1 PSR");
   hlprpc->SetTitle("PseudoRapidity/Phi coordinates");
   return c3;
}
The following example shows the same histogram as a surface plot is the four
different coordinates systems.


Picture
Source



output of MACRO_THistPainter_59_c4


{
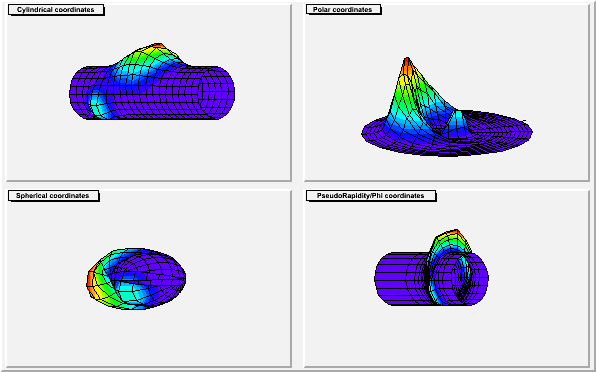
   TCanvas *c4 = new TCanvas("c4","c4",600,400);
   c4->Divide(2,2);
   TH2F *hscc = new TH2F("hscc","Cylindrical coordinates",20,-4,4,20,-20,20);
   Float_t px, py;
   for (Int_t i = 0; i < 25000; i++) {
      gRandom->Rannor(px,py);
      hscc->Fill(px-1,5*py);
      hscc->Fill(2+0.5*px,2*py-10.,0.1);
   }
   gStyle->SetPalette(1);
   c4->cd(1) ; hscc->Draw("SURF1 CYL");
   c4->cd(2) ; TH2F *hspc = hscc->DrawClone("SURF1 POL");
   hspc->SetTitle("Polar coordinates");
   c4->cd(3) ; TH2F *hssc = hscc->DrawClone("SURF1 SPH");
   hssc->SetTitle("Spherical coordinates");
   c4->cd(4) ; TH2F *hsprpc = hscc->DrawClone("SURF1 PSR");
   hsprpc->SetTitle("PseudoRapidity/Phi coordinates");
   return c4;
}
Base line for bar-charts and lego plots

By default the base line used to draw the boxes for bar-charts and lego plots is
the histogram minimum. It is possible to force this base line to be 0 with the
command:

      gStyle->SetHistMinimumZero();




Picture
Source



output of MACRO_THistPainter_61_c5


{
   TCanvas *c5 = new TCanvas("c5","c5",700,400);
   c5->Divide(2,1);
   gStyle->SetHistMinimumZero(1);
   TH1F *hz1 = new TH1F("hz1","Bar-chart drawn from 0",20,-3,3);
   TH2F *hz2 = new TH2F("hz2","Lego plot drawn from 0",20,-3,3,20,-3,3);
   Int_t i;
   Double_t x,y;
   hz1->SetFillColor(kBlue);
   hz2->SetFillColor(kBlue);
   for (i=0;i<10000;i++) {
      x = gRandom->Gaus(0,1);
      y = gRandom->Gaus(0,1);
      if (x>0) {
         hz1->Fill(x,1);
         hz2->Fill(x,y,1);
      } else {
         hz1->Fill(x,-1);
         hz2->Fill(x,y,-2);
      }
   }
   c5->cd(1); hz1->Draw("bar2");
   c5->cd(2); hz2->Draw("lego1");
   return c5;
}
The SPEC option

This option allows to use the TSpectrum2Painter tools. See the full
documentation in TSpectrum2Painter::PaintSpectrum.

Option "Z" : Adding the color palette on the right side of the pad

When this option is specified, a color palette with an axis indicating the value
of the corresponding color is drawn on the right side of the picture. In case,
not enough space is left, one can increase the size of the right margin by
calling TPad::SetRightMargin(). The attributes used to display the
palette axis values are taken from the Z axis of the object. For example, to
set the labels size on the palette axis do:

      hist->GetZaxis()->SetLabelSize().


WARNING: The palette axis is always drawn vertically.

Setting the color palette

To change the color palette TStyle::SetPalette should be used, eg:

      gStyle->SetPalette(ncolors,colors);


For example the option "COL" draws a 2D histogram with cells
represented by a box filled with a color index which is a function
of the cell content.
If the cell content is N, the color index used will be the color number
in colors[N], etc. If the maximum cell content is greater than
ncolors, all cell contents are scaled to ncolors.

If  ncolors <= 0, a default palette (see below) of 50 colors is
defined. This palette is recommended for pads, labels ...

If ncolors == 1 && colors == 0, a pretty palette with a violet to
red spectrum is created. It is recommended you use this palette when drawing
legos, surfaces or contours.

If ncolors > 50 and colors=0, the DeepSea palette is used.
(see TStyle::CreateGradientColorTable for more details)

 If ncolors > 0 && colors == 0, the default palette is used
with a maximum of ncolors.

 The default palette defines:

    

  •  index  0  to  9 : shades of grey

  •  index 10  to 19 : shades of brown

  •  index 20  to 29 : shades of blue

  •  index 30  to 39 : shades of red

  •  index 40  to 49 : basic colors


The color numbers specified in the palette can be viewed by selecting
the item "colors" in the "VIEW" menu of the canvas tool bar.
The red, green, and blue components of a color can be changed thanks to
TColor::SetRGB().

Drawing a sub-range of a 2D histogram; the [cutg] option

Using a TCutG object, it is possible to draw a sub-range of a 2D
histogram. One must create a graphical cut (mouse or C++) and specify the name
of the cut between [] in the Draw() option.
For example, with a TCutG named "cutg", one can call:

      myhist->Draw("surf1 [cutg]");


To invert the cut, it is enough to put a "-" in front of its name:

      myhist->Draw("surf1 [-cutg]");


It is possible to apply several cuts ("," means logical AND):

      myhist->Draw("surf1 [cutg1,cutg2]");




Picture
Source



output of MACRO_THistPainter_63_c1_n8


#include "TF2.h"
#include "TH2.h"
#include "TCutG.h"
#include "TMath.h"

// This tutorial illustrates :
//  - how to create a 2-d function
//  - fill a 2-d histogram randomly from this function
//  - fit the histogram
//  - display the fitted function on top of the histogram (lego-plot)
//    using a surface plot in a sub-range of the histogram.
//
// This example can be executed via the interpreter or/and the compiler
//   root > .x fit2a.C
//   root > .x fit2a.C++
//Author: Rene Brun
         
Double_t g2(Double_t *x, Double_t *par) {
   Double_t r1 = Double_t((x[0]-par[1])/par[2]);
   Double_t r2 = Double_t((x[1]-par[3])/par[4]);
   return par[0]*TMath::Exp(-0.5*(r1*r1+r2*r2));
}   
Double_t fun2(Double_t *x, Double_t *par) {
   Double_t *p1 = &par[0];
   Double_t *p2 = &par[5];
   Double_t *p3 = &par[10];
   Double_t result = g2(x,p1) + g2(x,p2) + g2(x,p3);
   return result;
}

TCanvas *fit2a() {
   TCanvas *c = new TCanvas();
   gStyle->SetOptStat(kTRUE); 
   gStyle->SetPalette(1); 
   const Int_t npar = 15;
   Double_t f2params[npar] = {100,-3,3,-3,3,160,0,0.8,0,0.9,40,4,0.7,4,0.7};
   TF2 *f2 = new TF2("f2",fun2,-10,10,-10,10, npar);
   f2->SetParameters(f2params);

   //Create an histogram and fill it randomly with f2
   TH2F *h2 = new TH2F("h2","From f2",40,-10,10,40,-10,10);
   Int_t nentries = 100000;
   h2->FillRandom("f2",nentries);
   //Fit h2 with original function f2
   Float_t ratio = 4*nentries/100000;
   f2params[ 0] *= ratio;
   f2params[ 5] *= ratio;
   f2params[10] *= ratio;
   f2->SetParameters(f2params);
   h2->Fit("f2","N");
   TCutG *cutg = new TCutG("cutg",5);
   cutg->SetPoint(0,-7,-7);
   cutg->SetPoint(1, 2,-7);
   cutg->SetPoint(2, 2, 2);
   cutg->SetPoint(3,-7, 2);
   cutg->SetPoint(4,-7,-7);
   h2->Draw("lego2 0");
   h2->SetFillColor(38);
   f2->SetNpx(80);
   f2->SetNpy(80);
   f2->Draw("surf1 same bb [cutg]");
   return c;
}
Drawing options for 3D histograms




"ISO"
Draw a Gouraud shaded 3d iso surface through a 3d histogram. It paints one
surface at the value computed as follow:
SumOfWeights/(NbinsX*NbinsY*NbinsZ)



"BOX"
Draw a for each cell with volume proportional to the content's absolute value.




By default, like 2D histograms, 3D histograms are drawn as scatter plots.

The following example shows a 3D histogram plotted as a scatter plot.


Picture
Source



output of MACRO_THistPainter_65_c06


{
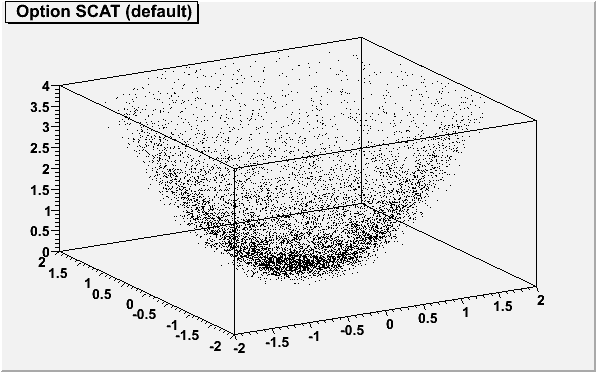
   TCanvas *c06 = new TCanvas("c06","c06",600,400);
   gStyle->SetOptStat(kFALSE);
   TH3F *h3scat = new TH3F("h3scat","Option SCAT (default) ",15,-2,2,15,-2,2,15,0,4);
   Double_t x, y, z;
   for (Int_t i=0;i<10000;i++) {
      gRandom->Rannor(x, y);
      z = x*x + y*y;
      h3scat->Fill(x,y,z);
   }
   h3scat->Draw();
   return c06;
}
The following example shows a 3D histogram plotted with the option "BOX".


Picture
Source



output of MACRO_THistPainter_67_c16


{
   TCanvas *c16 = new TCanvas("c16","c16",600,400);
   gStyle->SetOptStat(kFALSE);
   TH3F *h3box = new TH3F("h3box","Option BOX",15,-2,2,15,-2,2,15,0,4);
   Double_t x, y, z;
   for (Int_t i=0;i<10000;i++) {
      gRandom->Rannor(x, y);
      z = x*x + y*y;
      h3box->Fill(x,y,z);
   }
   h3box->Draw("BOX");
   return c16;
}
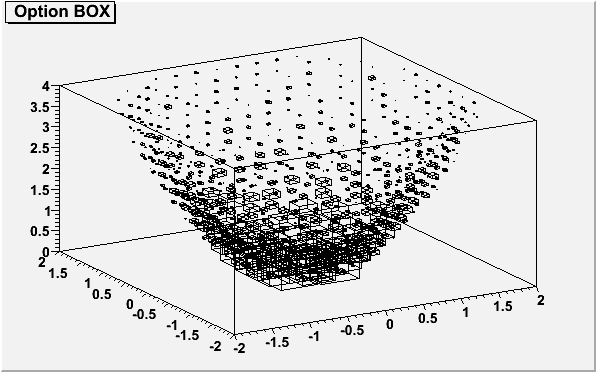
The following example shows a 3D histogram plotted with the option "BOX".


Picture
Source



output of MACRO_THistPainter_69_c26


{
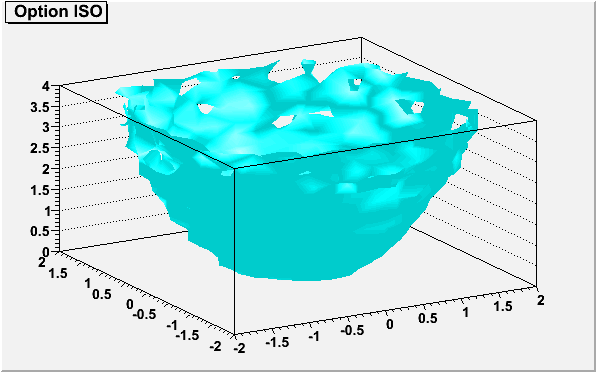
   TCanvas *c26 = new TCanvas("c26","c26",600,400);
   gStyle->SetOptStat(kFALSE);
   TH3F *h3iso = new TH3F("h3iso","Option ISO",15,-2,2,15,-2,2,15,0,4);
   Double_t x, y, z;
   for (Int_t i=0;i<10000;i++) {
      gRandom->Rannor(x, y);
      z = x*x + y*y;
      h3iso->Fill(x,y,z);
   }
   h3iso->SetFillColor(kCyan);
   h3iso->Draw("ISO");
   return c26;
}
Drawing option for histograms' stacks

Stacks of histograms are managed with the THStack. A THStack
is a collection of TH1 (or derived) objects. For painting only the
THStack containing TH1 only or
THStack containing TH2 only will be considered.

By default, histograms are shown stacked:

    

  1.  The first histogram is paint.

  2.  The the sum of the first and second, etc...


If option "NOSTACK" is specified, histograms are all paint in the
same pad as if the option "SAME" had been specified.

If option "PADS" is specified, the current pad/canvas is subdivided
into a number of pads equal to the number of histograms and each histogram
is paint into a separate pad.

The following example shows various types of stacks.


Picture
Source



output of MACRO_THistPainter_71_cst


TCanvas *hstack() {
// Example of stacked histograms: class THStack
//
//  Author: Rene Brun
   
   THStack *hs = new THStack("hs","Stacked 1D histograms");
   //create three 1-d histograms
   TH1F *h1st = new TH1F("h1st","test hstack",100,-4,4);
   h1st->FillRandom("gaus",20000);
   h1st->SetFillColor(kRed);
   h1st->SetMarkerStyle(21);
   h1st->SetMarkerColor(kRed);
   hs->Add(h1st);
   TH1F *h2st = new TH1F("h2st","test hstack",100,-4,4);
   h2st->FillRandom("gaus",15000);
   h2st->SetFillColor(kBlue);
   h2st->SetMarkerStyle(21);
   h2st->SetMarkerColor(kBlue);
   hs->Add(h2st);
   TH1F *h3st = new TH1F("h3st","test hstack",100,-4,4);
   h3st->FillRandom("gaus",10000);
   h3st->SetFillColor(kGreen);
   h3st->SetMarkerStyle(21);
   h3st->SetMarkerColor(kGreen);
   hs->Add(h3st);
   
   TCanvas *cst = new TCanvas("cst","stacked hists",10,10,700,700);
   cst->SetFillColor(41);
   cst->Divide(2,2);
   // in top left pad, draw the stack with defaults
   cst->cd(1);
   hs->Draw();
   // in top right pad, draw the stack in non-stack mode and errors option
   cst->cd(2);
   gPad->SetGrid();
   hs->Draw("nostack,e1p");
   //in bottom left, draw in stack mode with "lego1" option
   cst->cd(3);
   gPad->SetFrameFillColor(17);
   gPad->SetTheta(3.77);
   gPad->SetPhi(2.9);
   hs->Draw("lego1");

   cst->cd(4);
   //create two 2-D histograms and draw them in stack mode
   gPad->SetFrameFillColor(17);
   THStack *a = new THStack("a","Stacked 2D histograms");
   TF2 *f1 = new TF2("f1","xygaus + xygaus(5) + xylandau(10)",-4,4,-4,4);
   Double_t params[] = {130,-1.4,1.8,1.5,1, 150,2,0.5,-2,0.5, 3600,-2,0.7,-3,0.3};
   f1->SetParameters(params);
   TH2F *h2sta = new TH2F("h2sta","h2sta",20,-4,4,20,-4,4);
   h2sta->SetFillColor(38);
   h2sta->FillRandom("f1",4000);
   TF2 *f2 = new TF2("f2","xygaus + xygaus(5)",-4,4,-4,4);
   Double_t params[] = {100,-1.4,1.9,1.1,2, 80,2,0.7,-2,0.5};
   f2->SetParameters(params);
   TH2F *h2stb = new TH2F("h2stb","h2stb",20,-4,4,20,-4,4);
   h2stb->SetFillColor(46);
   h2stb->FillRandom("f2",3000);
   a->Add(h2sta);
   a->Add(h2stb);
   a->Draw();
   return cst;
}
Drawing of 3D implicit functions

3D implicit functions (TF3) can be drawn the following way:


Picture
Source



output of MACRO_THistPainter_73_c2


{
   TCanvas *c2 = new TCanvas("c2","c2",600,400);
   TF3 *f3 = new TF3("f3","sin(x*x+y*y+z*z-36)",-2,2,-2,2,-2,2);
   f3->SetClippingBoxOn(0,0,0);
   f3->SetFillColor(30);
   f3->SetLineColor(15);
   f3->Draw("FBBB");
   return c2;
}
Associated functions drawing

An associated function is created by TH1::Fit. More than on fitted
function can be associated with one histogram (see TH1::Fit).

A TF1 object f1 can be added to the list of associated
functions of an histogram h without calling TH1::Fit
simply doing:

      h->GetListOfFunctions()->Add(f1);


or

      h->GetListOfFunctions()->Add(f1,someoption);


To retrieve a function by name from this list, do:

      TF1 *f1 = (TF1*)h->GetListOfFunctions()->FindObject(name);


or

      TF1 *f1 = h->GetFunction(name);


Associated functions are automatically painted when an histogram is drawn.
To avoid the painting of the associated functions the option HIST
should be added to the list of the options used to paint the histogram.

Drawing using OpenGL

The class TGLHistPainter allows to paint data set using the OpenGL 3D
graphics library. The plotting options start with GL keyword.
In addition, in order to inform canvases that OpenGL should be used to render
3D representations, the following option should be set:

      gStyle->SetCanvasPreferGL(true);



General information: plot types and supported options

The following types of plots are provided:

For lego plots the supported options are:



"GLLEGO"
Draw a lego plot.



"GLLEGO2
Bins with color levels.



"GLLEGO3
Cylindrical bars.





Lego painter in cartesian supports logarithmic scales for X, Y, Z.
In polar only Z axis can be logarithmic, in cylindrical only Y.

For surface plots (TF2 and TH2) the supported options are:



"GLSURF" 
Draw a surface.



"GLSURF1"
Surface with color levels



"GLSURF2"
The same as "GLSURF1" but without polygon outlines.



"GLSURF3"
Color level projection on top of plot (works only in cartesian coordinate
system).



"GLSURF4"
Same as "GLSURF" but without polygon outlines.




The surface painting in cartesian coordinates supports logarithmic scales along
X, Y, Z axis. In polar coordinates only the Z axis can be logarithmic,
in cylindrical coordinates only the Y axis.

Additional options to SURF and LEGO - Coordinate systems:



" "
Default, cartesian coordinates system.



"POL"
Polar coordinates system.



"CYL"
Cylindrical coordinates system.



"SPH"
Spherical coordinates system.





TH3 as boxes (spheres)

The supported options are:



GLBOX" 
TH3 as a set of boxes, size of box is proportional to bin content.



GLBOX1"
The same as "glbox", but spheres are drawn instead of boxes.





TH3 as iso-surface(s)

The supported option is:



"GLISO" 
TH3 is drawn using iso-surfaces.





TF3 (implicit function)

The supported option is:



GLTF3" 
Draw a TF3.





Parametric surfaces

$ROOTSYS/tutorials/gl/glparametric.C shows how to create parametric
equations and visualize the surface.

Interaction with the plots

All the interactions are implemented via standard methods
DistancetoPrimitive() and ExecuteEvent(). That's why all the
interactions with the OpenGL plots are possible only when the mouse cursor is
in the plot's area (the plot's area is the part of a the pad occupied by
gl-produced picture). If the mouse cursor is not above gl-picture, the standard
pad interaction is performed.

Selectable parts

Different parts of the plot can be selected:

    

  •  xoz, yoz, xoy back planes:
When such a plane selected, it's highlighted in green if the
dynamic slicing by this plane is supported, and it's
highlighted in red, if the dynamic slicing is not supported.

  •  The plot itself:
On surfaces, the selected surface is outlined in red. (TF3 and
ISO are not outlined). On lego plots, the selected bin is
highlighted. The bin number and content are displayed in pad's
status bar. In box plots, the box or sphere is highlighted and
the bin info is displayed in pad's status bar.



Rotation and zooming


    

  • Rotation:
When the plot is selected, it can be rotated by pressing and
holding the left mouse button and move the cursor.

  • Zoom/Unzoom:
Mouse wheel or 'j', 'J', 'k', 'K' keys.



Panning

The selected plot can be moved in a pad's area by pressing and
holding the left mouse button and the shift key.

Box cut

Surface, iso, box, TF3 and parametric painters support box cut by
pressing the 'c' or 'C' key when the mouse cursor is in a plot's
area. That will display a transparent box, cutting away part of the
surface (or boxes) in order to show internal part of plot. This box
can be moved inside the plot's area (the full size of the box is
equal to the plot's surrounding box) by selecting one of the box
cut axes and pressing the left mouse button to move it.

Plot specific interactions (dynamic slicing etc.)

Currently, all gl-plots support some form of slicing. When back plane
is selected (and if it's highlighted in green) you can press and hold
left mouse button and shift key and move this back plane inside
plot's area, creating the slice. During this "slicing" plot becomes
semi-transparent. To remove all slices (and projected curves for
surfaces) double click with left mouse button in a plot's area.

Surface with option "GLSURF"

The surface profile is displayed on the slicing plane.
The profile projection is drawn on the back plane
by pressing 'p' or 'P' key.

TF3

The contour plot is drawn on the slicing plane. For TF3 the color
scheme can be changed by pressing 's' or 'S'.

Box

The contour plot corresponding to slice plane position is drawn in real time.

Iso

Slicing is similar to "GLBOX" option.

Parametric plot

No slicing. Additional keys: 's' or 'S' to change color scheme -
about 20 color schemes supported ('s' for "scheme"); 'l' or 'L' to
increase number of polygons ('l' for "level" of details), 'w' or 'W'
to show outlines ('w' for "wireframe").

 








Function Members (Methods)


public:



THistPainter()


THistPainter(const THistPainter&)


 virtual~THistPainter()


voidTObject::AbstractMethod(const char* method) const


virtual voidTObject::AppendPad(Option_t* option = "")


virtual voidTObject::Browse(TBrowser* b)


static TClass*Class()


virtual const char*TObject::ClassName() const


virtual voidTObject::Clear(Option_t* = "")


virtual TObject*TObject::Clone(const char* newname = "") const


virtual Int_tTObject::Compare(const TObject* obj) const


virtual voidTObject::Copy(TObject& object) const


virtual voidDefineColorLevels(Int_t ndivz)


virtual voidTObject::Delete(Option_t* option = "")MENU 


virtual Int_tDistancetoPrimitive(Int_t px, Int_t py)


virtual voidTObject::Draw(Option_t* option = "")


virtual voidTObject::DrawClass() constMENU 


virtual TObject*TObject::DrawClone(Option_t* option = "") constMENU 


virtual voidDrawPanel()


virtual voidTObject::Dump() constMENU 


virtual voidTObject::Error(const char* method, const char* msgfmt) const


virtual voidTObject::Execute(const char* method, const char* params, Int_t* error = 0)


virtual voidTObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0)


virtual voidExecuteEvent(Int_t event, Int_t px, Int_t py)


virtual voidTObject::Fatal(const char* method, const char* msgfmt) const


virtual TObject*TObject::FindObject(const char* name) const


virtual TObject*TObject::FindObject(const TObject* obj) const


static const char*GetBestFormat(Double_t v, Double_t e, const char* f)


virtual TList*GetContourList(Double_t contour) const


virtual Option_t*TObject::GetDrawOption() const


static Long_tTObject::GetDtorOnly()


virtual const char*TObject::GetIconName() const


virtual const char*TObject::GetName() const


virtual char*GetObjectInfo(Int_t px, Int_t py) const


static Bool_tTObject::GetObjectStat()


virtual Option_t*TObject::GetOption() const


virtual TList*GetStack() const


virtual const char*TObject::GetTitle() const


virtual UInt_tTObject::GetUniqueID() const


virtual Bool_tTObject::HandleTimer(TTimer* timer)


virtual ULong_tTObject::Hash() const


static TVirtualHistPainter*TVirtualHistPainter::HistPainter(TH1* obj)


virtual voidTObject::Info(const char* method, const char* msgfmt) const


virtual Bool_tTObject::InheritsFrom(const char* classname) const


virtual Bool_tTObject::InheritsFrom(const TClass* cl) const


virtual voidTObject::Inspect() constMENU 


voidTObject::InvertBit(UInt_t f)


virtual TClass*IsA() const


virtual Bool_tTObject::IsEqual(const TObject* obj) const


virtual Bool_tTObject::IsFolder() const


virtual Bool_tIsInside(Int_t x, Int_t y)


virtual Bool_tIsInside(Double_t x, Double_t y)


Bool_tTObject::IsOnHeap() const


virtual Bool_tTObject::IsSortable() const


Bool_tTObject::IsZombie() const


virtual voidTObject::ls(Option_t* option = "") const


virtual Int_tMakeChopt(Option_t* option)


virtual Int_tMakeCuts(char* cutsopt)


voidTObject::MayNotUse(const char* method) const


virtual Bool_tTObject::Notify()


static voidTObject::operator delete(void* ptr)


static voidTObject::operator delete(void* ptr, void* vp)


static voidTObject::operator delete[](void* ptr)


static voidTObject::operator delete[](void* ptr, void* vp)


void*TObject::operator new(size_t sz)


void*TObject::operator new(size_t sz, void* vp)


void*TObject::operator new[](size_t sz)


void*TObject::operator new[](size_t sz, void* vp)


THistPainter&operator=(const THistPainter&)


virtual voidPaint(Option_t* option = "")


virtual voidPaint2DErrors(Option_t* option)


virtual voidPaintArrows(Option_t* option)


virtual voidPaintAxis(Bool_t drawGridOnly = kFALSE)


virtual voidPaintBar(Option_t* option)


virtual voidPaintBarH(Option_t* option)


virtual voidPaintBoxes(Option_t* option)


virtual voidPaintColorLevels(Option_t* option)


virtual voidPaintContour(Option_t* option)


virtual Int_tPaintContourLine(Double_t elev1, Int_t icont1, Double_t x1, Double_t y1, Double_t elev2, Int_t icont2, Double_t x2, Double_t y2, Double_t* xarr, Double_t* yarr, Int_t* itarr, Double_t* levels)


virtual voidPaintErrors(Option_t* option)


virtual voidPaintFrame()


virtual voidPaintFunction(Option_t* option)


virtual voidPaintH3(Option_t* option = "")


virtual voidPaintH3Iso()


virtual voidPaintHist(Option_t* option)


virtual Int_tPaintInit()


virtual Int_tPaintInitH()


virtual voidPaintLego(Option_t* option)


virtual voidPaintLegoAxis(TGaxis* axis, Double_t ang)


virtual voidPaintPalette()


virtual voidPaintScatterPlot(Option_t* option)


static voidPaintSpecialObjects(const TObject* obj, Option_t* option)


virtual voidPaintStat(Int_t dostat, TF1* fit)


virtual voidPaintStat2(Int_t dostat, TF1* fit)


virtual voidPaintStat3(Int_t dostat, TF1* fit)


virtual voidPaintSurface(Option_t* option)


virtual voidPaintTable(Option_t* option)


virtual voidPaintText(Option_t* option)


virtual voidPaintTF3()


virtual voidPaintTitle()


virtual voidPaintTriangles(Option_t* option)


virtual voidTObject::Pop()


virtual voidTObject::Print(Option_t* option = "") const


virtual voidProcessMessage(const char* mess, const TObject* obj)


static Int_tProjectAitoff2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


static Int_tProjectMercator2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


static Int_tProjectParabolic2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


static Int_tProjectSinusoidal2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


virtual Int_tTObject::Read(const char* name)


virtual voidRecalculateRange()


virtual voidRecursiveRemove(TObject*)


voidTObject::ResetBit(UInt_t f)


virtual voidTObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU 


virtual voidTObject::SavePrimitive(basic_ostream<char,char_traits<char> >& out, Option_t* option = "")


voidTObject::SetBit(UInt_t f)


voidTObject::SetBit(UInt_t f, Bool_t set)


virtual voidTObject::SetDrawOption(Option_t* option = "")MENU 


static voidTObject::SetDtorOnly(void* obj)


virtual voidSetHistogram(TH1* h)


static voidTObject::SetObjectStat(Bool_t stat)


static voidTVirtualHistPainter::SetPainter(const char* painter)


virtual voidSetShowProjection(const char* option, Int_t nbins)


virtual voidSetStack(TList* stack)


virtual voidTObject::SetUniqueID(UInt_t uid)


virtual voidShowMembers(TMemberInspector& insp, char* parent)


virtual voidShowProjection3(Int_t px, Int_t py)


virtual voidShowProjectionX(Int_t px, Int_t py)


virtual voidShowProjectionY(Int_t px, Int_t py)


virtual voidStreamer(TBuffer& b)


voidStreamerNVirtual(TBuffer& b)


virtual voidTObject::SysError(const char* method, const char* msgfmt) const


virtual Int_tTableInit()


Bool_tTObject::TestBit(UInt_t f) const


Int_tTObject::TestBits(UInt_t f) const


virtual voidTObject::UseCurrentStyle()


virtual voidTObject::Warning(const char* method, const char* msgfmt) const


virtual Int_tTObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0)


virtual Int_tTObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const





protected:



virtual voidTObject::DoError(int level, const char* location, const char* fmt, va_list va) const


voidTObject::MakeZombie()










Data Members


public:



enum TObject::EStatusBits { kCanDelete


kMustCleanup


kObjInCanvas


kIsReferenced


kHasUUID


kCannotPick


kNoContextMenu


kInvalidObject


};


enum TObject::[unnamed] { kIsOnHeap


kNotDeleted


kZombie


kBitMask


kSingleKey


kOverwrite


kWriteDelete


};





protected:



TCutG*fCuts[16]Pointers to graphical cuts


Int_tfCutsOpt[16]sign of each cut


TList*fFunctionspointer to histogram list of functions


TGraph2DPainter*fGraph2DPainterpointer to a TGraph2DPainter object


TH1*fHpointer to histogram to paint


TPainter3dAlgorithms*fLegopointer to a TPainter3dAlgorithms object


Int_tfNcutsNumber of graphical cuts


TPie*fPiepointer to a TPie in case of option PIE


TStringfShowOptionOption to draw the projection


Int_tfShowProjectionTrue if a projection must be drawn


TList*fStackPointer to stack of histograms (if any)


TAxis*fXaxispointer to X axis


Double_t*fXbufX buffer coordinates


TAxis*fYaxispointer to Y axis


Double_t*fYbufY buffer coordinates


TAxis*fZaxispointer to Z axis







Class Charts

























Inheritance
Inherited Members
Includes
Libraries



Class Charts


Function documentation


 THistPainter(const THistPainter& )


   Default constructor.
   

 





 ~THistPainter()


   Default destructor.
   

 





Int_t DistancetoPrimitive(Int_t px, Int_t py)


   Compute the distance from the point px,py to a line.
   

   Compute the closest distance of approach from point px,py to elements of
   an histogram. The distance is computed in pixels units.
   

   Algorithm:

   Currently, this simple model computes the distance from the mouse to the
   histogram contour only.
   

 





void DrawPanel()


   Display a panel with all histogram drawing options.
   

 





void ExecuteEvent(Int_t event, Int_t px, Int_t py)


   Execute the actions corresponding to "event".
   

   This function is called when a histogram is clicked with the locator at
   the pixel position px,py.
   

 





TList * GetContourList(Double_t contour) const


   Get a contour (as a list of TGraphs) using the Delaunay triangulation.
   

 





char * GetObjectInfo(Int_t px, Int_t py) const


   Display the histogram info (bin number, contents, integral up to bin
   corresponding to cursor position px,py.
   

 





Bool_t IsInside(Int_t ix, Int_t iy)


   Return kTRUE if the cell ix, iy is inside one of the graphical cuts.
   

 





Bool_t IsInside(Double_t x, Double_t y)


   Return kTRUE if the point x,y is inside one of the graphical cuts.
   

 





Int_t MakeChopt(Option_t* option)


   Decode string "choptin" and fill Hoption structure.
   

 





Int_t MakeCuts(char* cutsopt)


   Decode string "choptin" and fill Graphical cuts structure.
   

 





void Paint(Option_t* option = "")


   Control routine to paint any kind of histograms.
   

 





void PaintArrows(Option_t* option)


   Control function to draw a table as an arrow plot.
   

 





void PaintAxis(Bool_t drawGridOnly = kFALSE)


   Draw axis (2D case) of an histogram.
   

   If drawGridOnly is TRUE, only the grid is painted (if needed). This allows
   to draw the grid and the axis separately. In THistPainter::Paint this
   feature is used to make sure that the grid is drawn in the background and
   the axis tick marks in the foreground of the pad.
   

 





void PaintBar(Option_t* option)


   Draw a bar-chart in a normal pad.
   

 





void PaintBarH(Option_t* option)


   Draw a bar char in a rotated pad (X vertical, Y horizontal).
   

 





void PaintBoxes(Option_t* option)


   Control function to draw a 2D histogram as a box plot.
   

 





void PaintColorLevels(Option_t* option)


   Control function to draw a 2D histogram as a color plot.
   

 





void PaintContour(Option_t* option)


   Control function to draw a 2D histogram as a contour plot.
   

 





Int_t PaintContourLine(Double_t elev1, Int_t icont1, Double_t x1, Double_t y1, Double_t elev2, Int_t icont2, Double_t x2, Double_t y2, Double_t* xarr, Double_t* yarr, Int_t* itarr, Double_t* levels)


   Fill the matrix XARR YARR for Contour Plot.
   

 





void PaintErrors(Option_t* option)


   Draw 1D histograms error bars.
   

 





void Paint2DErrors(Option_t* option)


   Draw 2D histograms errors.
   

 





void PaintFrame()


   Calculate range and clear pad (canvas).
   

 





void PaintFunction(Option_t* option)


   Paint functions associated to an histogram.
   

 





void PaintHist(Option_t* option)


   Control routine to draw 1D histograms.
   

 





void PaintH3(Option_t* option = "")


   Control function to draw a 3D histograms.
   

 





Int_t PaintInit()


   Compute histogram parameters used by the drawing routines.
   

 





Int_t PaintInitH()


   Compute histogram parameters used by the drawing routines for a rotated pad.
   

 





void PaintH3Iso()


   Control function to draw a 3D histogram with Iso Surfaces.
   

 





void PaintLego(Option_t* option)


   Control function to draw a 2D histogram as a lego plot.
   

 





void PaintLegoAxis(TGaxis* axis, Double_t ang)


   Draw the axis for legos and surface plots.
   

 





void PaintPalette()


   Paint the color palette on the right side of the pad.
   

 





void PaintScatterPlot(Option_t* option)


   Control function to draw a 2D histogram as a scatter plot.
   

 





void PaintSpecialObjects(const TObject* obj, Option_t* option)


   Static function to paint special objects like vectors and matrices.
   This function is called via gROOT->ProcessLine to paint these objects
   without having a direct dependency of the graphics or histogramming
   system.
   

 





void PaintStat(Int_t dostat, TF1* fit)


   Draw the statistics box for 1D and profile histograms.
   

 





void PaintStat2(Int_t dostat, TF1* fit)


   Draw the statistics box for 2D histograms.
   

 





void PaintStat3(Int_t dostat, TF1* fit)


   Draw the statistics box for 3D histograms.
   

 





void PaintSurface(Option_t* option)


   Control function to draw a 2D histogram as a surface plot.
   

 





void PaintTriangles(Option_t* option)


   Control function to draw a table using Delaunay triangles.
   

 





void DefineColorLevels(Int_t ndivz)


   Define the color levels used to paint legos, surfaces etc..
   

 





void PaintTable(Option_t* option)


   Control function to draw 2D/3D histograms (tables).
   

 





void PaintText(Option_t* option)


   Control function to draw a 1D/2D histograms with the bin values.
   

 





void PaintTF3()


   Control function to draw a 3D implicit functions.
   

 





void PaintTitle()


   Draw the histogram title
   

   The title is drawn according to the title alignment returned by
   GetTitleAlign(). It is a 2 digits integer): hv
   

   where "h" is the horizontal alignment and "v" is the
   vertical alignment.
   

   for instance the default alignment is: 13 (left top)
   

 





void ProcessMessage(const char* mess, const TObject* obj)


    Process message "mess".
   

 





Int_t ProjectAitoff2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


   Static function.

   Convert Right Ascension, Declination to X,Y using an AITOFF projection.
   This procedure can be used to create an all-sky map in Galactic
   coordinates with an equal-area Aitoff projection.  Output map
   coordinates are zero longitude centered.
   Also called Hammer-Aitoff projection (first presented by Ernst von Hammer in 1892)
   

   source: GMT

   code from  Ernst-Jan Buis
   

 





Int_t ProjectMercator2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


   Static function 

   Probably the most famous of the various map projections, the Mercator projection
   takes its name from Mercator who presented it in 1569. It is a cylindrical, conformal projection
   with no distortion along the equator.
   The Mercator projection has been used extensively for world maps in which the distortion towards
   the polar regions grows rather large, thus incorrectly giving the impression that, for example,
   Greenland is larger than South America. In reality, the latter is about eight times the size of
   Greenland. Also, the Former Soviet Union looks much bigger than Africa or South America. One may wonder
   whether this illusion has had any influence on U.S. foreign policy.' (Source: GMT)
   code from  Ernst-Jan Buis
   

 





Int_t ProjectSinusoidal2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


   Static function code from  Ernst-Jan Buis
   

 





Int_t ProjectParabolic2xy(Double_t l, Double_t b, Double_t& Al, Double_t& Ab)


   Static function code from  Ernst-Jan Buis
   

 





void RecalculateRange()


   Recompute the histogram range following graphics operations.
   

 





void SetHistogram(TH1* h)


   Set current histogram to "h".
   

 





Int_t TableInit()


   Initialize various options to draw 2D histograms.
   

 





const char * GetBestFormat(Double_t v, Double_t e, const char* f)


   This function returns the best format to print the error value (e)
   knowing the parameter value (v) and the format (f) used to print it.
   

 





void SetShowProjection(const char* option, Int_t nbins)


   Set projection.
   

 





void ShowProjectionX(Int_t px, Int_t py)


   Show projection onto X.
   

 





void ShowProjectionY(Int_t px, Int_t py)


   Show projection onto Y.
   

 





void ShowProjection3(Int_t px, Int_t py)


   Show projection (specified by fShowProjection) of a TH3.
   The drawing option for the projection is in fShowOption.
   

   First implementation; R.Brun 

   Full implementation: Tim Tran (timtran@jlab.org)  April 2006
   

 





 THistPainter(const THistPainter& )




TList     * GetStack()



{return fStack;}






void RecursiveRemove(TObject* )



{;}






void SetStack(TList* stack)



{fStack = stack;}









Author:  Rene Brun   26/08/99

Last change: root/histpainter:$Id: THistPainter.h 25489 2008-09-22 13:05:29Z brun $

Last generated: 2008-11-21 15:27

Copyright   (C) 1995-2000, Rene Brun and Fons Rademakers.               *




This page has been automatically generated. If you have any comments or suggestions about the page layout send a mail to ROOT support, or contact the developers with any questions or problems regarding ROOT.