How to estimate parameters of a sinogram for a shifted PET ring
Unshifted PET
Normally, sinogram parameters p and $\varphi$ in a normal ring with crystals spaced $\Delta\varphi$ appart depend solely on crystal indices $i$ and $j$. Assuming the crystals are labelled from 0 to N-1 circumferrentially, ignoring for a second their variable axial offset. The tangens of the azimuthal angle $\varphi$ equals to the ratio of the vertical and horizontal distance between the crystals that interacted:
$$\tan\varphi=\frac{\Delta y}{\Delta x}$$
The figure shows the layout:
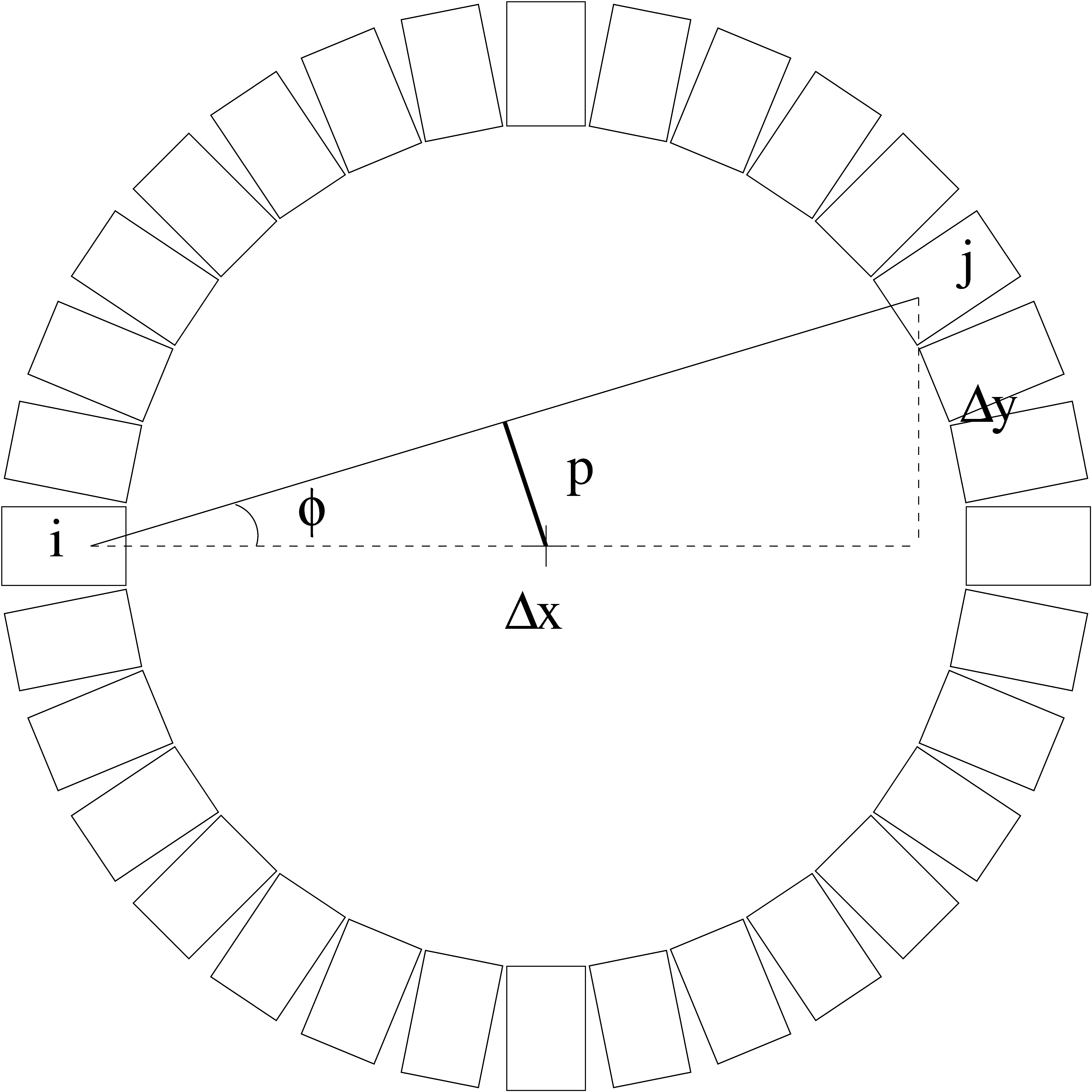
As crystals are laid out in a ring, their locations are simply $R(\cos\varphi_i,\sin\varphi_i$), and
$$\varphi_i=(i+0.5)\Delta\varphi$$
is the position of the center of the i-th crystal. Since R appears both in numerator and denominator of the $\varphi$ expression, it cancels out:
$$ \tan\varphi = \frac{\sin\varphi_j-\sin\varphi_i} {\cos\varphi_j-\cos\varphi_i} $$
Using trigonometric identities, we get:
$$ \tan\varphi= \arctan(-\frac{\varphi_i+\varphi_j}{2}) =\tan((2k+1)\frac{\pi}{2}+\frac{\varphi_i+\varphi_j}{2}) $$
or equivalently:
$$\varphi=(2k+1)\frac{\pi}{2}+(i+j+1)\frac{\Delta\varphi}{2}$$
The arbitrary integer can be selected to adjust the range of values for $\varphi$. Normally, the range $[0,\pi]$ is selected, requiring k to change for different (i,j) combinations. The following ranges are handled by the following constants:
- $i+j<\frac{N}{2}-1$, k=0 and $\varphi$ is in $[\frac{\pi}{2},\pi]$
- $\frac{N}{2}-1<i+j<N-1$, k=-1 and $\varphi$ is in $[0,\frac{\pi}{2}]$
- $N-1<i+j<3\frac{N}{2}-1$, k=-1 and $\varphi$ is in $[\frac{\pi}{2},\pi]$
- $3\frac{N}{2}-1<i+j<2N-1$, k=-2 and $\varphi$ is in $[0,\frac{\pi}{2}]$
Given azimuthal angle $\varphi$ and an arbitrary point (x,y) on the LOR, the offset (tangential) parameter of the LOR is given as:
$$p=x\sin\varphi-y\cos\varphi$$
Inserting $R(\cos\varphi_i,\sin\varphi_i)$ as (x,y) and applying trigonometry, we get:
$$p=R\sin((2k+1)\frac{\pi}{2}+(j-i)\frac{\Delta\varphi}{2}) =R(-1)^k\cos((j-i)\frac{\Delta\varphi}{2})$$
Because $\cos$ is an even function, symmetry under index exchange $i\leftrightarrow j$ is explicit. Also:
$$p=R(-1)^k\sin(\frac{\pi}{2}+(j-i)\frac{\Delta\varphi}{2})$$
Motivated by the above expression, parameter $\delta_I$ is introduced with I noting a particular combination of indices i and j:
$$\delta_I=j-(i-\frac{\pi}{\Delta\varphi}),$$
equal to 0 for crystals exactly opposite in the ring. We also use $\delta$ to modify the $\varphi$ expression, where a total offset of $\phi$ can be ignored, since reconstruction is identical for $\pi$ shifted LORs. Then we have:
$$p_I=R(-1)^k\sin(\delta_I\frac{\Delta\varphi}{2})$$
$$\varphi_I=k\pi+i\Delta\varphi+(\delta_I+1)\frac{\Delta\varphi}{2}$$
The first summand in $\varphi_I$ can be viewed as an offset expression - in uncomplete rings where object is rotated, this term becomes the sum of the object rotation and the crystal offset. The expression is symmetric in i and j (to the ignored offset of $\pi$), so ordering of the hit crystals within the LOR is unimportant (for 2D!).
Both $\varphi_I$ and $p_I$ can only assume a set of discrete values. For $\varphi_I$ the values are multiples of $\Delta\varphi/2$:
$$\varphi_I=0,\frac{\Delta\varphi}{2},\Delta\varphi, \frac{3}{2}\Delta\varphi,\dots,\pi-\frac{\Delta\varphi}{2}$$
Expressing as
$$\varphi_m=m\frac{\Delta\varphi}{2}$$
where m is an integer, we can label azimuthal bins. In each bin m there are a number of measurements for $p_I$, since $\delta_I$=m-2i-kN-1. Because of the 2 factor before the i, $\delta_I$ can only be odd for even M, and even for odd M. For small $\delta_I$ the sine can be expanded via Taylor series to be equal to the angle itself; then the tangential parameter can be expressed as:
$$p_n=n\frac{R\Delta\varphi}{2}$$
where n is an integer. The expression $R\Delta\varphi$ is to a good approximation equal to circumferrential crystal size $c$, hence:
$$p_n=n\frac{c}{2}$$
giving us a natural bin size in p. Because of the odd/even pattern, the sinogram binned to $c/2$ in p and $\Delta\varphi/2$ in $\varphi$ will have a characteristic checkboard pattern. To avoid it, sinograms are often interleaved in angle, making angular bins twice the size ($\Delta\varphi$) and half the number, which in principle doesn't deteriorate scanner's resolution.